Bipolar coordinate system

savecancel

Yes one can use bipolar coordinates in SageMath provided that one sets by hand the relations between bipolar and Cartesian coordinates, as follows. First, we introduce the Euclidean plane $E$ with the default Cartesian coordinates $(x,y)$:

sage: E.<x,y> = EuclideanSpace()
sage: CA = E.cartesian_coordinates(); CA
Chart (E^2, (x, y))

We then declare the bipolar coordinates $(\tau, \sigma)$ as a new chart on $E$:

sage: BP.<t,s> = E.chart(r"t:\tau s:\sigma:(-pi,pi)")
sage: BP
Chart (E^2, (t, s))
sage: BP.coord_range()
t: (-oo, +oo); s: (-pi, pi)

We set the transformation from the bipolar coordinates to the Cartesian ones, using e.g. the Wikipedia formulas. This involves $\cosh\tau$ and $\sinh\tau$. For the ease of automatic simplifications, we prefer the exponential representation of cosh and sinh:

sage: cosht = (exp(t) + exp(-t))/2
sage: sinht = (exp(t) - exp(-t))/2
sage: BP_to_CA = BP.transition_map(CA, [sinht/(cosht - cos(s)), sin(s)/(cosht - cos(s))])
sage: BP_to_CA.display()
x = (e^(-t) - e^t)/(2*cos(s) - e^(-t) - e^t)
y = -2*sin(s)/(2*cos(s) - e^(-t) - e^t)

We also provide the inverse transformation:

sage: BP_to_CA.set_inverse(1/2*ln(((x+1)^2 + y^2)/((x-1)^2 + y^2)), 
....:                      pi - 2*atan(2*y/(1-x^2-y^2+sqrt((1-x^2-y^2)^2 + 4*y^2))))
sage: BP_to_CA.inverse().display()
t = 1/2*log(((x + 1)^2 + y^2)/((x - 1)^2 + y^2))
s = pi - 2*arctan(-2*y/(x^2 + y^2 - sqrt((x^2 + y^2 - 1)^2 + 4*y^2) - 1))

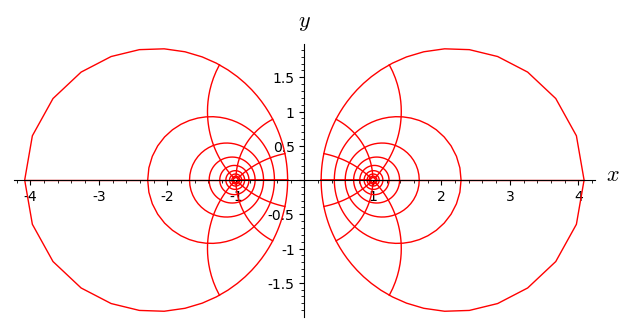
At this stage, we may plot the grid of bipolar coordinates in terms of the Cartesian coordinates (the plot is split in 2 parts to avoid $\tau = 0$):

sage: BP.plot(CA, ranges={t: (-4, -0.5)}) + BP.plot(CA, ranges={t: (0.5, 4)})

Let us do some calculus with bipolar coordinates. The Euclidean metric is

sage: g = E.metric()
sage: g.display()
g = dx*dx + dy*dy

From here, we declare that the default coordinates are the bipolar ones:

sage: E.set_default_chart(BP)
sage: E.set_default_frame(BP.frame())

We have then:

sage: g.display()
g = -4*e^(2*t)/(4*cos(s)*e^(3*t) - 2*(2*cos(s)^2 + 1)*e^(2*t) + 4*cos(s)*e^t - e^(4*t) - 1) dt*dt 
     - 4*e^(2*t)/(4*cos(s)*e^(3*t) - 2*(2*cos(s)^2 + 1)*e^(2*t) + 4*cos(s)*e^t - e^(4*t) - 1) ds*ds

Let us factor the metric coefficients to get a shorter expression:

sage: g[1,1].factor()
4*e^(2*t)/(2*cos(s)*e^t - e^(2*t) - 1)^2
sage: g[2,2].factor()
4*e^(2*t)/(2*cos(s)*e^t - e^(2*t) - 1)^2
sage: g.display()
g = 4*e^(2*t)/(2*cos(s)*e^t - e^(2*t) - 1)^2 dt*dt 
  + 4*e^(2*t)/(2*cos(s)*e^t - e^(2*t) - 1)^2 ds*ds

We can check the identity (cf. the Wikipedia page):

sage: g[1,1] == 1/(cosht - cos(s))^2
True

Let us consider a generic scalar field on $E$, defined by a function $F$ of the bipolar coordinates:

sage: f = E.scalar_field({BP: function('F')(t,s)}, name='f')
sage: f.display(BP)
f: E^2 --> R
   (t, s) |--> F(t, s)

The expression of the Laplacian of $f$ in bipolar coordinates is

sage: f.laplacian().expr(BP).factor()
1/4*(2*cos(s)*e^t - e^(2*t) - 1)^2*(diff(F(t, s), t, t) + diff(F(t, s), s, s))*e^(-2*t)

Again it agrees with that given in the Wikipedia page.

The gradient of $f$ is

sage: f.gradient().display()
grad(f) = -1/4*(4*cos(s)*e^(3*t) - 2*(2*cos(s)^2 + 1)*e^(2*t) + 4*cos(s)*e^t - e^(4*t) - 1)*e^(-2*t)*d(F)/dt d/dt
         - 1/4*(4*cos(s)*e^(3*t) - 2*(2*cos(s)^2 + 1)*e^(2*t) + 4*cos(s)*e^t - e^(4*t) - 1)*e^(-2*t)*d(F)/ds d/ds