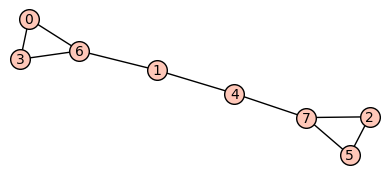
The following code loops over the graphs(8) generator, eliminates the graphs that are not connected, then those that have a cycle basis with either more or less than two cycles (hope this corresponds to what is wanted, please chech this point), then puts in a list the (tuple assembling the) algebraic connectivity together with the full graph. This redundant information is then sorted, sorting is done w.r.t. the first entry of the tuple, this is the algebraic connectivity. At the end, i am printing the first five hits after sorting.
import networkx
count = 0
g_data_list = []
format_string = 'Graph # {} with algebraic connectivity = {}\n{!r}\n'
for g in graphs(8):
if not g.is_connected():
continue
g_cycle_basis = g.cycle_basis()
if len(g_cycle_basis) != 2:
continue
# ok, here we are in business
count += 1
ng = networkx.Graph(g.to_dictionary())
ag = networkx.algebraic_connectivity(ng)
# print(format_string.format(count, ag, g.adjacency_matrix()))
g_data_list.append((ag, g))
g_data_list.sort()
# show the first three entries in the list
count = 0
for ag, g in g_data_list[:5]:
count += 1
print(format_string.format(count, ag, g.adjacency_matrix()))
Results:
Graph # 1 with algebraic connectivity = 0.186393497352
[0 0 0 1 0 0 1 0]
[0 0 0 0 1 0 1 0]
[0 0 0 0 0 1 0 1]
[1 0 0 0 0 0 1 0]
[0 1 0 0 0 0 0 1]
[0 0 1 0 0 0 0 1]
[1 1 0 1 0 0 0 0]
[0 0 1 0 1 1 0 0]
Graph # 2 with algebraic connectivity = 0.193041644941
[0 0 0 1 0 1 0 1]
[0 0 0 0 1 0 1 0]
[0 0 0 0 0 0 1 1]
[1 0 0 0 0 1 0 1]
[0 1 0 0 0 0 0 0]
[1 0 0 1 0 0 0 0]
[0 1 1 0 0 0 0 0]
[1 0 1 1 0 0 0 0]
Graph # 3 with algebraic connectivity = 0.202256672304
[0 0 0 0 1 1 0 0]
[0 0 0 0 0 1 0 1]
[0 0 0 0 0 0 1 1]
[0 0 0 0 0 0 1 1]
[1 0 0 0 0 0 0 0]
[1 1 0 0 0 0 0 0]
[0 0 1 1 0 0 0 1]
[0 1 1 1 0 0 1 0]
Graph # 4 with algebraic connectivity = 0.218346547469
[0 0 0 0 1 0 1 0]
[0 0 0 0 0 1 1 0]
[0 0 0 0 0 1 0 1]
[0 0 0 0 0 0 0 1]
[1 0 0 0 0 0 1 0]
[0 1 1 0 0 0 0 1]
[1 1 0 0 1 0 0 0]
[0 0 1 1 0 1 0 0]
Graph # 5 with algebraic connectivity = 0.224287144264
[0 0 0 0 1 0 0 1]
[0 0 0 0 0 1 1 0]
[0 0 0 0 0 1 1 0]
[0 0 0 0 0 0 1 1]
[1 0 0 0 0 0 0 1]
[0 1 1 0 0 0 0 0]
[0 1 1 1 0 0 0 0]
[1 0 0 1 1 0 0 0]
And the winner is:
sage: g_data_list[0][1].show()
Launched png viewer for Graphics object consisting of 18 graphics primitives