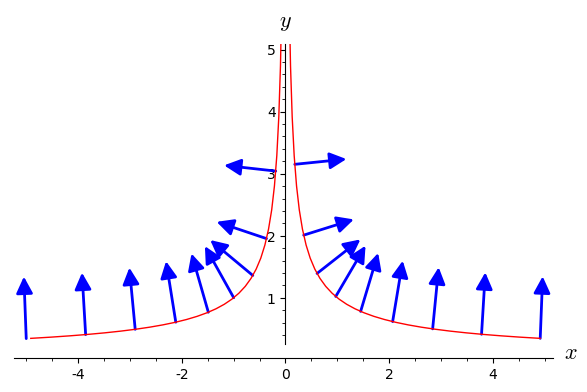
Restriction of domain of vector field

edit

I was trying to plot a field of normal vectors to a given implicit graph. What I got so far is:

x, y = var('x y')
f(x,y) = 2*x*y^3
g(x,y) = x^2*3*y^2
d = plot_vector_field((f(x,y)/sqrt(f(x,y)^2+g(x,y)^2),g(x,y)/sqrt(f(x,y)^2+g(x,y)^2)), (x,-5,5), (y,-5,5))
s = implicit_plot(x^2*y^3-1 , (x,-5,5), (y,-5,5))
show(s+d)

And it works like a charm, however, is there a way to "restrict" a domain of plot_vector_field so it doesn't plot all the vectors in a given range, but only for point (x,y) lying on my graph? That is such points that x^2*y^3=1. I tried to just put it instead (y,-5,5) (in a y=(1/x^2)^(1/3) form), but it obviously doesn't work. Thx for any help as I'm new to Sage.