I want to have a finite graph G on 10 vertices in my latex document. I thought the easiest way to get it is to first draw it sage notebook using the graph_editor(). Then use latex(G) to get the latex code and copy and paste it. But when I do this, I keep getting errors. It says undefined control sequence for \Vertex..
Is there any example which will walk me through these steps? Many thanks for your help,
To do it that way, you need to use the package tkz-graph, by adding the following to the header of your LaTeX file:
\usepackage{tkz-graph}
On Debian GNU/Linux (or Ubuntu), you have to install the texlive-pictures package
For more details, see:
sage: sage.graphs.graph_latex?
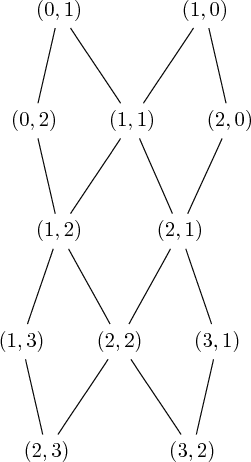
After installing dot2tex with
sage -i dot2tex
and with graphviz installed, you may create a tikzpicture from the positions of vertices decided by graphviz:
sage: G = graphs.AztecDiamondGraph(2)
sage: G.latex_options().set_options(format='dot2tex', prog='dot', edge_labels=True, color_by_label=False)
The tikzpicture code is:
sage: latex(G)
\begin{tikzpicture}[>=latex,line join=bevel,]
%%
\node (node_9) at (26.5bp,8.5bp) [draw,draw=none] {$\left(2, 3\right)$};
\node (node_8) at (61.5bp,61.5bp) [draw,draw=none] {$\left(2, 2\right)$};
\node (node_7) at (90.5bp,114.5bp) [draw,draw=none] {$\left(2, 1\right)$};
\node (node_6) at (114.5bp,167.5bp) [draw,draw=none] {$\left(2, 0\right)$};
\node (node_5) at (14.5bp,61.5bp) [draw,draw=none] {$\left(1, 3\right)$};
\node (node_4) at (32.5bp,114.5bp) [draw,draw=none] {$\left(1, 2\right)$};
\node (node_3) at (67.5bp,167.5bp) [draw,draw=none] {$\left(1, 1\right)$};
\node (node_2) at (102.5bp,220.5bp) [draw,draw=none] {$\left(1, 0\right)$};
\node (node_1) at (20.5bp,167.5bp) [draw,draw=none] {$\left(0, 2\right)$};
\node (node_0) at (32.5bp,220.5bp) [draw,draw=none] {$\left(0, 1\right)$};
\node (node_11) at (96.5bp,8.5bp) [draw,draw=none] {$\left(3, 2\right)$};
\node (node_10) at (108.5bp,61.5bp) [draw,draw=none] {$\left(3, 1\right)$};
\draw [black,] (node_0) ..controls (44.282bp,202.33bp) and (55.687bp,185.71bp) .. (node_3);
\draw [black,] (node_4) ..controls (42.262bp,96.332bp) and (51.712bp,79.713bp) .. (node_8);
\draw [black,] (node_4) ..controls (26.441bp,96.332bp) and (20.575bp,79.713bp) .. (node_5);
\draw [black,] (node_8) ..controls (49.718bp,43.332bp) and (38.313bp,26.713bp) .. (node_9);
\draw [black,] (node_3) ..controls (55.718bp,149.33bp) and (44.313bp,132.71bp) .. (node_4);
\draw [black,] (node_6) ..controls (106.42bp,149.33bp) and (98.6bp,132.71bp) .. (node_7);
\draw [black,] (node_5) ..controls (18.539bp,43.332bp) and (22.45bp,26.713bp) .. (node_9);
\draw [black,] (node_8) ..controls (73.282bp,43.332bp) and (84.687bp,26.713bp) .. (node_11);
\draw [black,] (node_1) ..controls (24.539bp,149.33bp) and (28.45bp,132.71bp) .. (node_4);
\draw [black,] (node_2) ..controls (90.718bp,202.33bp) and (79.313bp,185.71bp) .. (node_3);
\draw [black,] (node_7) ..controls (80.738bp,96.332bp) and (71.288bp,79.713bp) .. (node_8);
\draw [black,] (node_2) ..controls (106.54bp,202.33bp) and (110.45bp,185.71bp) .. (node_6);
\draw [black,] (node_0) ..controls (28.461bp,202.33bp) and (24.55bp,185.71bp) .. (node_1);
\draw [black,] (node_10) ..controls (104.46bp,43.332bp) and (100.55bp,26.713bp) .. (node_11);
\draw [black,] (node_7) ..controls (96.559bp,96.332bp) and (102.42bp,79.713bp) .. (node_10);
\draw [black,] (node_3) ..controls (75.242bp,149.33bp) and (82.737bp,132.71bp) .. (node_7);
%
\end{tikzpicture}
You may get a preview:
sage: view(G)
Asked: 2017-11-11 05:54:21 +0100
Seen: 673 times
Last updated: Nov 11 '17
Copyright Sage, 2010. Some rights reserved under creative commons license. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.
