Weird resulting values with an exponential regression
I have this model:
var('a,b')
R = [[100, 0.0489], [110, 0.0633], [120, 0.1213],[130, 0.1244], [140, 0.1569], [150, 0.1693], [160, 0.3154], [170, 0.6146], [180, 0.9118], [190, 01.7478], [200, 2.4523], [210, 4.7945], [230, 17.9766], [240, 29.3237], [250, 52.4374], [260, 94.6463], [270, 173.3447], [280, 396.0443], [290, 538.6976], [300, 1118.9984], [310, 1442.3694], [320, 4151.9089], [330, 6940.7322]]
model(x) = a*exp(b*x)
find_fit(R,model)
(which is the results of factorization time of an algorithm for people interested)
But I get weird values, obviously not in accordance with the points, when plotting all this. I was extremely surprised. That's what I get:
[a=(2.3863359829×10^−15),b=1.0000000003]
Then I had the idea to try to get a formula with LibreOffice calc, just to have something to compare (I wasn't about to do this work on libreoffice initially), the result is different, but still so weird. In both cases, if I apply the formula given, it returns unthinkable values (very high).
Seems to be a problem with these values, no? Impossible to compute? Does sb have a solution? Thank you.

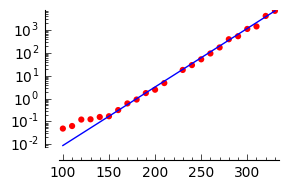

This seems to be the same problem in Scipy as http://ask.sagemath.org/question/2643...
Really? That's annoying... By the way the SageMathCell gives the same thing. I think it must be the programs, not powerful enough (or the algorithms) to work with exponentials, big amount of data... that's delicate as a function. I've experienced similar problems in python (not with math and regressions): it was supposed to work fine and there were errors no one could understand. Weird problems, in short...
The result of FindFit[] in Mathematica 10 is
{a -> 0., b -> 1.}That doesn't really help -- and th'at's also false.
I think paulmasson's point was that it means this is the kind of data that standard regression models don't do well with in general...