Revision history [back]
 | 1 | initial version |
Complement to Max's and Tolga's comments :
sage: var("t")
t
sage: with assuming(x>1): (e^(t^2)/sqrt(t)).integrate(t, 1, x^2)
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
$$ -\frac{1}{2} \, \left(-1\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -1\right) + \frac{\left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{3}} $$
As you can see, this expression involves different inherently non-real complex factors (fractional powers of negative numbers, $\Gamma$ with negative arguments), whose sums happens to be real. The computation of the numerical value is inexact, so a small inexactitude is enough to result in a numerically non-zero imaginary part.
Showing that this imaginary part is zero seems out of reach of current CASses...
 | 2 | No.2 Revision |
Complement to Max's and Tolga's comments :
sage: var("t")
t
sage: with assuming(x>1): (e^(t^2)/sqrt(t)).integrate(t, 1, x^2)
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
$$ -\frac{1}{2} \, \left(-1\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -1\right) + \frac{\left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{3}} $$
As you can see, this expression involves different inherently non-real complex factors (fractional powers of negative numbers, $\Gamma$ with negative arguments), whose sums happens to be real. The computation of the numerical value is inexact, so a small inexactitude is enough to result in a numerically non-zero imaginary part.
Showing that this imaginary part is zero seems out of reach of current CASses...
EDIT : To illistrate Max's comment about derivation :
sage: with assuming(x>1): foo=(e^(t^2)/sqrt(t)).integrate(t, 1, x^2) ; foo
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
sage: foo.diff(x)
-2*(-x^4)^(3/4)*D[1](gamma)(1/4, -x^4) - 3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
$$ -2 \, \left(-x^{4}\right)^{\frac{3}{4}} \mathrm{D}_{1}\left(\Gamma\right)\left(\frac{1}{4}, -x^{4}\right) - \frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} $$
 | 3 | No.3 Revision |
Complement to Max's and Tolga's comments :
sage: var("t")
t
sage: with assuming(x>1): (e^(t^2)/sqrt(t)).integrate(t, 1, x^2)
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
$$ -\frac{1}{2} \, \left(-1\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -1\right) + \frac{\left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{3}} $$
As you can see, this expression involves different inherently non-real complex factors (fractional powers of negative numbers, $\Gamma$ with negative arguments), whose sums happens to be real. The computation of the numerical value is inexact, so a small inexactitude is enough to result in a numerically non-zero imaginary part.
Showing that this imaginary part is zero seems out of reach of current CASses...
EDIT : To illistrate Max's comment about derivation :
sage: with assuming(x>1): foo=(e^(t^2)/sqrt(t)).integrate(t, 1, x^2) ; foo
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
sage: foo.diff(x)
-2*(-x^4)^(3/4)*D[1](gamma)(1/4, -x^4) - 3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
$$ -2 \, \left(-x^{4}\right)^{\frac{3}{4}} \mathrm{D}_{1}\left(\Gamma\right)\left(\frac{1}{4}, -x^{4}\right) - \frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} $$
One notes that Sage does not explicites a derivative of $\Gamma$ wrt one of its arguments... Neither does Mathematica :
sage: foo._mathematica_().diff(x)
diff[-1/2*((-1)^(3/4)*Gamma[1/4, -1]) + ((-x^4)^(3/4)*Gamma[1/4, -x^4])/
(2*x^3), x]
Suspicious :
sage: giac.diff(*map(giac, (foo, x)))._sage_()
-3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4 + 2*e^(x^4)
$$ -\frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} + 2 \, e^{\left(x^{4}\right)} $$
Highly suspicious :
sage: fricas.D(*map(fricas, (foo, x)))._sage_()
2*e^(x^4)
But these expressions tun out to be equal :
sage: (fricas.D(*map(fricas, (foo, x)))._sage_()-giac.diff(*map(giac, (foo, x)))._sage_())
3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) + 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
sage: (fricas.D(*map(fricas, (foo, x)))._sage_()-giac.diff(*map(giac, (foo, x)))._sage_()).factor()
0
and comparing the Fricas result to a (rough) numerical estimate of the derivative of the function shows a very good agreement : their quotient is 1 up to $10^-6$ on the range (1, 4) :
sage: plot(lambda u:((Foo(u+1e-8)-Foo(u))/1e-8).real()/(2*e^(u^4))-1, (1, 4))
Launched png viewer for Graphics object consisting of 1 graphics primitive
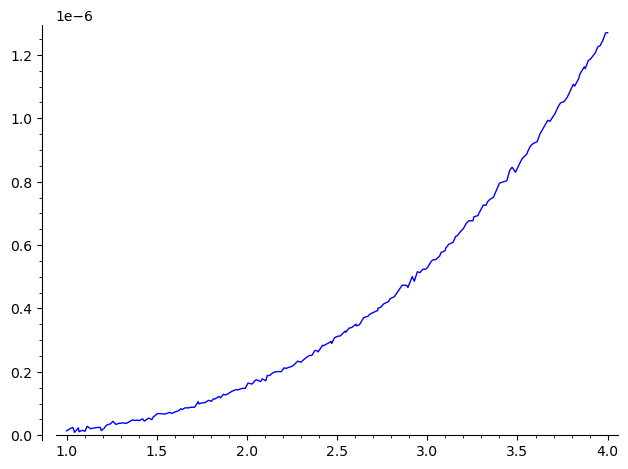
Frcas' and Giac's derivations seem to be exact. The Sage's $\Gamma$ implementation may be perfected...
HTH,
 | 4 | No.4 Revision |
Complement to Max's and Tolga's comments :
sage: var("t")
t
sage: with assuming(x>1): (e^(t^2)/sqrt(t)).integrate(t, 1, x^2)
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
$$ -\frac{1}{2} \, \left(-1\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -1\right) + \frac{\left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{3}} $$
As you can see, this expression involves different inherently non-real complex factors (fractional powers of negative numbers, $\Gamma$ with negative arguments), whose sums happens to be real. The computation of the numerical value is inexact, so a small inexactitude is enough to result in a numerically non-zero imaginary part.
Showing that this imaginary part is zero seems out of reach of current CASses...
EDIT : To illistrate Max's comment about derivation :
sage: with assuming(x>1): foo=(e^(t^2)/sqrt(t)).integrate(t, 1, x^2) ; foo
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
sage: foo.diff(x)
-2*(-x^4)^(3/4)*D[1](gamma)(1/4, -x^4) - 3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
$$ -2 \, \left(-x^{4}\right)^{\frac{3}{4}} \mathrm{D}_{1}\left(\Gamma\right)\left(\frac{1}{4}, -x^{4}\right) - \frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} $$
One notes that Sage does not explicites a derivative of $\Gamma$ wrt one of its arguments... Neither does Mathematica :
sage: foo._mathematica_().diff(x)
diff[-1/2*((-1)^(3/4)*Gamma[1/4, -1]) + ((-x^4)^(3/4)*Gamma[1/4, -x^4])/
(2*x^3), x]
Suspicious :
sage: giac.diff(*map(giac, (foo, x)))._sage_()
-3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4 + 2*e^(x^4)
$$ -\frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} + 2 \, e^{\left(x^{4}\right)} $$
Highly suspicious :
sage: fricas.D(*map(fricas, (foo, x)))._sage_()
2*e^(x^4)
But these expressions tun out to be equal :
sage: (fricas.D(*map(fricas, (foo, x)))._sage_()-giac.diff(*map(giac, (foo, x)))._sage_())
3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) + 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
sage: (fricas.D(*map(fricas, (foo, x)))._sage_()-giac.diff(*map(giac, (foo, x)))._sage_()).factor()
0
and comparing the Fricas result to a (rough) numerical estimate of the derivative of the function shows a very good agreement : their quotient is 1 up to $10^-6$ $10^{-6}$ on the range (1, 4) :
sage: plot(lambda u:((Foo(u+1e-8)-Foo(u))/1e-8).real()/(2*e^(u^4))-1, (1, 4))
Launched png viewer for Graphics object consisting of 1 graphics primitive

Frcas' and Giac's derivations seem to be exact. The Sage's $\Gamma$ implementation may be perfected...
HTH,
 | 5 | No.5 Revision |
Complement to Max's and Tolga's comments :
sage: var("t")
t
sage: with assuming(x>1): (e^(t^2)/sqrt(t)).integrate(t, 1, x^2)
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
$$ -\frac{1}{2} \, \left(-1\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -1\right) + \frac{\left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{3}} $$
As you can see, this expression involves different inherently non-real complex factors (fractional powers of negative numbers, $\Gamma$ with negative arguments), whose sums happens to be real. The computation of the numerical value is inexact, so a small inexactitude is enough to result in a numerically non-zero imaginary part.
Showing that this imaginary part is zero seems out of reach of current CASses...
EDIT : To illistrate Max's comment about derivation :
sage: with assuming(x>1): foo=(e^(t^2)/sqrt(t)).integrate(t, 1, x^2) ; foo
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
sage: foo.diff(x)
-2*(-x^4)^(3/4)*D[1](gamma)(1/4, -x^4) - 3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
$$ -2 \, \left(-x^{4}\right)^{\frac{3}{4}} \mathrm{D}_{1}\left(\Gamma\right)\left(\frac{1}{4}, -x^{4}\right) - \frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} $$
One notes that Sage does not explicites a derivative of $\Gamma$ wrt one of its arguments... Neither does Mathematica :
sage: foo._mathematica_().diff(x)
diff[-1/2*((-1)^(3/4)*Gamma[1/4, -1]) + ((-x^4)^(3/4)*Gamma[1/4, -x^4])/
(2*x^3), x]
Suspicious :
sage: giac.diff(*map(giac, (foo, x)))._sage_()
-3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4 + 2*e^(x^4)
$$ -\frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} + 2 \, e^{\left(x^{4}\right)} $$
Highly suspicious :
sage: fricas.D(*map(fricas, (foo, x)))._sage_()
2*e^(x^4)
and, BTW :
sage: foo._sympy_().diff(x._sympy_())._sage_()
2*e^(x^4)
sage: foo._mathematica_().D(x).FullSimplify().sage()
2*e^(x^4)
But these expressions tun out to be equal :
sage: (fricas.D(*map(fricas, (foo, x)))._sage_()-giac.diff(*map(giac, (foo, x)))._sage_())
3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) + 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
sage: (fricas.D(*map(fricas, (foo, x)))._sage_()-giac.diff(*map(giac, (foo, x)))._sage_()).factor()
0
and comparing the Fricas result to a (rough) numerical estimate of the derivative of the function shows a very good agreement : their quotient is 1 up to $10^{-6}$ on the range (1, 4) :
sage: plot(lambda u:((Foo(u+1e-8)-Foo(u))/1e-8).real()/(2*e^(u^4))-1, (1, 4))
Launched png viewer for Graphics object consisting of 1 graphics primitive

Frcas' Mathematica's, Fricas' and Giac's derivations seem to be exact. The Sage's $\Gamma$ implementation may be perfected...
HTH,
