Revision history [back]
 | 1 | initial version |
One possible way to do it :
nl=3
nc=2
ring=QQ
A=matrix(ring,nl,nc,[3,2,1,4,1,1])
b=vector(ring,[3,5,6])
c=vector(ring,[4,7])
# Use expressions rather than strings : more useful, less hassle.
# sign=list([">=",">=","<="])
# vsign=list([">=",">="])
from _operator import eq, le, lt, ge, gt
# Don't scratch built-in "sign" function, it may come handy later on
hsign = [ge, ge, le]
vsign = [ge, ge]
# show(LatexExpr(r"\boldsymbol{A}="),A)
# show(LatexExpr(r"\boldsymbol{b}="),b)
# show(LatexExpr(r"\boldsymbol{c}="),c)
# show(LatexExpr(r"\boldsymbol{Signs}="),sign)
# show(LatexExpr(r"\boldsymbol{Vsigns}="),vsign)
# Neither Python's max nor Sage's symbolic_max accept a single argument,
# and neither denote maximization. Let's use an ad hoc symbolic function
maximize = function("maximize",
print_latex_func=lambda self, *args:
r"\text{maximize}\ %s"%latex(args[0]))
def primal_lp(opt,A,b,c,signAb,signx):
nc=A.ncols()
x = var("x_", n=nc)
# X=[xj for xj in x] # This exact copy has no use.
# X replaced by x afterwards...
# Zer1 =[0 for v in x]
Zer1 = [0]*len(x) # faster
# Zer2 =[0 for v in range(len(signAb))]
Zer2 = [0]*len(signAb) # MUCH faster
con=A*vector(x)
# z=c*vector(x) # Used once, put it inline...
# from _operator import le, ge, eq # Done at toplevel
# No neeed since we use expressions
# op1=[ge if v==">=" else (le if v=='<=' else eq) for v in signx]
tt1=list(map(lambda u,v:u(*v), signx ,zip(x,Zer1)))
# Ditto
# op2=[ge if v==">=" else (le if v=='<=' else eq) for v in signAb]
tt2=list(map(lambda u,v:u(*v), signx ,zip(con,Zer2)))
# z1=flatten([opt,z,tt2,tt1])
# return show(z1)
z1 = [opt(c*vector(x))]+tt2+tt1
# If we want to return a table
# z1=table([[u] for u in tt2+tt1],
# header_row=[opt(c*vector(x))])
return z1
This returns a list of expressions :
sage: primal_lp(maximize,A,b,c,hsign,vsign)
[maximize(4*x_0 + 7*x_1),
3*x_0 + 2*x_1 >= 0,
x_0 + 4*x_1 >= 0,
x_0 >= 0,
x_1 >= 0]
whose tabulation is easy : view(table([[u] for u in primal_lp(maximize,A,b,c,hsign,vsign)])) will give you something like :
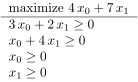
[ I had to recourse to image conversion, since ask.sagemath.org's damn Mathjax won't accept tabular expressions :
sage: print(latex(table([[u] for u in primal_lp(maximize,A,b,c,hsign,vsign)])))
\begin{tabular}{l}
$\text{maximize}\ 4 \, x_{0} + 7 \, x_{1}$ \\
$3 \, x_{0} + 2 \, x_{1} \geq 0$ \\
$x_{0} + 4 \, x_{1} \geq 0$ \\
$x_{0} \geq 0$ \\
$x_{1} \geq 0$ \\
\end{tabular}
]
HTH,
 | 2 | No.2 Revision |
One possible way to do it :
nl=3
nc=2
ring=QQ
A=matrix(ring,nl,nc,[3,2,1,4,1,1])
b=vector(ring,[3,5,6])
c=vector(ring,[4,7])
# Use expressions rather than strings : more useful, less hassle.
# sign=list([">=",">=","<="])
# vsign=list([">=",">="])
from _operator import eq, le, lt, ge, gt
# Don't scratch built-in "sign" function, it may come handy later on
hsign = [ge, ge, le]
vsign = [ge, ge]
# show(LatexExpr(r"\boldsymbol{A}="),A)
# show(LatexExpr(r"\boldsymbol{b}="),b)
# show(LatexExpr(r"\boldsymbol{c}="),c)
# show(LatexExpr(r"\boldsymbol{Signs}="),sign)
# show(LatexExpr(r"\boldsymbol{Vsigns}="),vsign)
# Neither Python's max nor Sage's symbolic_max accept a single argument,
# and neither denote maximization. Let's use an ad hoc symbolic function
maximize = function("maximize",
print_latex_func=lambda self, *args:
r"\text{maximize}\ %s"%latex(args[0]))
def primal_lp(opt,A,b,c,signAb,signx):
nc=A.ncols()
x = var("x_", n=nc)
# X=[xj for xj in x] # This exact copy has no use.
# X replaced by x afterwards...
# Zer1 =[0 for v in x]
Zer1 = [0]*len(x) # faster
# Zer2 =[0 for v in range(len(signAb))]
Zer2 = [0]*len(signAb) # MUCH faster
con=A*vector(x)
# z=c*vector(x) # Used once, put it inline...
# from _operator import le, ge, eq # Done at toplevel
# No neeed since we use expressions
# op1=[ge if v==">=" else (le if v=='<=' else eq) for v in signx]
tt1=list(map(lambda u,v:u(*v), signx ,zip(x,Zer1)))
# Ditto
# op2=[ge if v==">=" else (le if v=='<=' else eq) for v in signAb]
tt2=list(map(lambda u,v:u(*v), signx ,zip(con,Zer2)))
# z1=flatten([opt,z,tt2,tt1])
# return show(z1)
z1 = [opt(c*vector(x))]+tt2+tt1
# If we want to return a table
# z1=table([[u] for u in tt2+tt1],
# header_row=[opt(c*vector(x))])
return z1
This returns a list of expressions :
sage: primal_lp(maximize,A,b,c,hsign,vsign)
[maximize(4*x_0 + 7*x_1),
3*x_0 + 2*x_1 >= 0,
x_0 + 4*x_1 >= 0,
x_0 >= 0,
x_1 >= 0]
whose tabulation is easy : view(table([[u] for u in primal_lp(maximize,A,b,c,hsign,vsign)])) will give you something like :
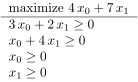
[ I had to recourse to image conversion, since ask.sagemath.org's damn Mathjax won't accept tabular expressions :
sage: print(latex(table([[u] for u in primal_lp(maximize,A,b,c,hsign,vsign)])))
\begin{tabular}{l}
$\text{maximize}\ 4 \, x_{0} + 7 \, x_{1}$ \\
$3 \, x_{0} + 2 \, x_{1} \geq 0$ \\
$x_{0} + 4 \, x_{1} \geq 0$ \\
$x_{0} \geq 0$ \\
$x_{1} \geq 0$ \\
\end{tabular}
]
HTH,
| \(\text{maximize}\ 4 \, x_{0} + 7 \, x_{1}\) |
| \(3 \, x_{0} + 2 \, x_{1} \geq 0\) |
| \(x_{0} + 4 \, x_{1} \geq 0\) |
| \(x_{0} \geq 0\) |
| \(x_{1} \geq 0\) |
 | 3 | No.3 Revision |
One possible way to do it :
nl=3
nc=2
ring=QQ
A=matrix(ring,nl,nc,[3,2,1,4,1,1])
b=vector(ring,[3,5,6])
c=vector(ring,[4,7])
# Use expressions rather than strings : more useful, less hassle.
# sign=list([">=",">=","<="])
# vsign=list([">=",">="])
from _operator import eq, le, lt, ge, gt
# Don't scratch built-in "sign" function, it may come handy later on
hsign = [ge, ge, le]
vsign = [ge, ge]
# show(LatexExpr(r"\boldsymbol{A}="),A)
# show(LatexExpr(r"\boldsymbol{b}="),b)
# show(LatexExpr(r"\boldsymbol{c}="),c)
# show(LatexExpr(r"\boldsymbol{Signs}="),sign)
# show(LatexExpr(r"\boldsymbol{Vsigns}="),vsign)
# Neither Python's max nor Sage's symbolic_max accept a single argument,
# and neither denote maximization. Let's use an ad hoc symbolic function
maximize = function("maximize",
print_latex_func=lambda self, *args:
r"\text{maximize}\ %s"%latex(args[0]))
def primal_lp(opt,A,b,c,signAb,signx):
nc=A.ncols()
x = var("x_", n=nc)
# X=[xj for xj in x] # This exact copy has no use.
# X replaced by x afterwards...
# Zer1 =[0 for v in x]
Zer1 = [0]*len(x) # faster
# Zer2 =[0 for v in range(len(signAb))]
Zer2 = [0]*len(signAb) # MUCH faster
con=A*vector(x)
# z=c*vector(x) # Used once, put it inline...
# from _operator import le, ge, eq # Done at toplevel
# No neeed since we use expressions
# op1=[ge if v==">=" else (le if v=='<=' else eq) for v in signx]
tt1=list(map(lambda u,v:u(*v), signx ,zip(x,Zer1)))
# Ditto
# op2=[ge if v==">=" else (le if v=='<=' else eq) for v in signAb]
tt2=list(map(lambda u,v:u(*v), signx ,zip(con,Zer2)))
# z1=flatten([opt,z,tt2,tt1])
# return show(z1)
z1 = [opt(c*vector(x))]+tt2+tt1
# If we want to return a table
# z1=table([[u] for u in tt2+tt1],
# header_row=[opt(c*vector(x))])
return z1
This returns a list of expressions :
sage: primal_lp(maximize,A,b,c,hsign,vsign)
[maximize(4*x_0 + 7*x_1),
3*x_0 + 2*x_1 >= 0,
x_0 + 4*x_1 >= 0,
x_0 >= 0,
x_1 >= 0]
whose tabulation is easy : view(table([[u] for u in primal_lp(maximize,A,b,c,hsign,vsign)])) will give you something like :
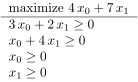
[ I had to recourse to image conversion, since ask.sagemath.org's damn Mathjax won't accept tabular expressions :
sage: print(latex(table([[u] for u in primal_lp(maximize,A,b,c,hsign,vsign)])))
\begin{tabular}{l}
$\text{maximize}\ 4 \, x_{0} + 7 \, x_{1}$ \\
$3 \, x_{0} + 2 \, x_{1} \geq 0$ \\
$x_{0} + 4 \, x_{1} \geq 0$ \\
$x_{0} \geq 0$ \\
$x_{1} \geq 0$ \\
\end{tabular}
]
HTH,
EDIT : slelievre's suggestion worked (on Sagecell), and gave the following result :
| \(\text{maximize}\ 4 \, x_{0} + 7 \, x_{1}\) |
| \(3 \, x_{0} + 2 \, x_{1} \geq 0\) |
| \(x_{0} + 4 \, x_{1} \geq 0\) |
| \(x_{0} \geq 0\) |
| \(x_{1} \geq 0\) |
