Revision history [back]
 | 1 | initial version |
Both answers are correct.
To see it by hand, we can use:
- (x+1)5/2=(x+1)(x+1)3/2=x(x+1)3/2+(x+1)3/2
- (x+1)3/2=(x+1)(x+1)1/2=x(x+1)1/2+(x+1)1/2
to express both as linear combinations of (x + 1)^(1/2) and x * (x + 1)^(1/2).
To see it with Sage, we can differentiate both and compare them.
Define the function to integrate:
sage: x = var('x')
sage: f = x*sqrt(x + 1)
sage: f
sqrt(x + 1)*xIntegrate with Sage:
sage: F = integral(f, x)
sage: F
2/5*(x + 1)^(5/2) - 2/3*(x + 1)^(3/2)The primitive you computed (up to a constant):
sage: G = (2/3)*x*(x + 1)^(3/2) - (4/15)*(x + 1)^(5/2)
sage: G
-4/15*(x + 1)^(5/2) + 2/3*(x + 1)^(3/2)*xTo see that they are both correct:
sage: bool(F == G)
TrueOr check they have the same derivative:
sage: g = G.diff(x)
sage: g
sqrt(x + 1)*x
sage: ff = F.diff(x)
sage: ff
(x + 1)^(3/2) - sqrt(x + 1)
sage: bool(g == ff)
TrueOr more visually, compare the plots of F and G (or f and ff):
sage: pF = plot(F, (-1, 1.6), color='firebrick')
sage: pG = plot(G, (-1, 1.6), color='steelblue')
sage: p = graphics_array([pF, pG, pF + pG])
sage: p.show(figsize=(7, 3))
Launched png viewer for Graphics Array of size 1 x 3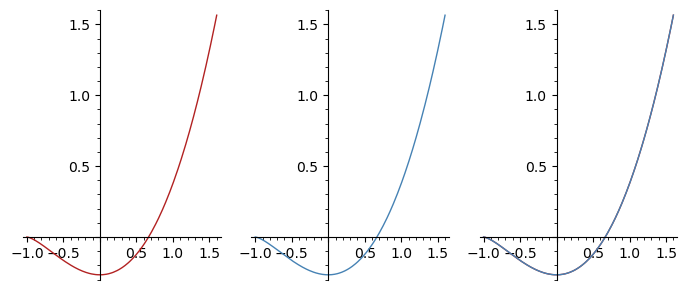
 | 2 | No.2 Revision |
Both answers are correct.
To see it by hand, we can use:
- (x+1)5/2=(x+1)(x+1)3/2=x(x+1)3/2+(x+1)3/2
- (x+1)3/2=(x+1)(x+1)1/2=x(x+1)1/2+(x+1)1/2
to express both as linear combinations of (x + 1)^(1/2) x * (x + 1)^(1/2).
To see it with Sage, we can differentiate both and compare them.
Define the function to integrate:
sage: x = var('x')
sage: f = x*sqrt(x + 1)
sage: f
sqrt(x + 1)*xIntegrate Compute a primitive (aka antiderivative) with Sage:
sage: F = integral(f, x)
sage: F
2/5*(x + 1)^(5/2) - 2/3*(x + 1)^(3/2)The primitive you computed (up to a constant):
sage: G = (2/3)*x*(x + 1)^(3/2) - (4/15)*(x + 1)^(5/2)
sage: G
-4/15*(x + 1)^(5/2) + 2/3*(x + 1)^(3/2)*xTo see Check that they are both correct:agree:
sage: bool(F == G)
TrueOr check Check they have the same derivative:
sage: g = G.diff(x)
sage: g
sqrt(x + 1)*x
sage: ff = F.diff(x)
sage: ff
(x + 1)^(3/2) - sqrt(x + 1)
sage: bool(g == ff)
TrueOr more visually, compare the plots of F and G (or f and ff):
sage: pF = plot(F, (-1, 1.6), color='firebrick')
sage: pG = plot(G, (-1, 1.6), color='steelblue')
sage: p = graphics_array([pF, pG, pF + pG])
sage: p.show(figsize=(7, 3))
Launched png viewer for Graphics Array of size 1 x 3
 | 3 | No.3 Revision |
Both answers are correct.
To see it by hand, we can use:
- (x+1)5/2=(x+1)(x+1)3/2=x(x+1)3/2+(x+1)3/2
- (x+1)3/2=(x+1)(x+1)1/2=x(x+1)1/2+(x+1)1/2
to express both as linear combinations of (x+1)1/2,
$x (x + 1)^1/2}$ 1)^{1/2}$ and x2(x+1)1/2.
To see it with Sage, we can can
- ask Sage whether the two different expressions in fact agree
- differentiate both and compare
them.them - plot the functions to visually check whether they agree
Define the function to integrate:
sage: x = var('x')
sage: f = x*sqrt(x + 1)
sage: f
sqrt(x + 1)*xCompute a primitive (aka antiderivative) with Sage:
sage: F = integral(f, x)
sage: F
2/5*(x + 1)^(5/2) - 2/3*(x + 1)^(3/2)The primitive you computed (up to a constant):
sage: G = (2/3)*x*(x + 1)^(3/2) - (4/15)*(x + 1)^(5/2)
sage: G
-4/15*(x + 1)^(5/2) + 2/3*(x + 1)^(3/2)*xCheck that they agree:
sage: bool(F == G)
TrueCheck they have the same derivative:
sage: g = G.diff(x)
sage: g
sqrt(x + 1)*x
sage: ff = F.diff(x)
sage: ff
(x + 1)^(3/2) - sqrt(x + 1)
sage: bool(g == ff)
TrueOr more visually, compare the plots of F and G (or f and ff):
sage: pF = plot(F, (-1, 1.6), color='firebrick')
sage: pG = plot(G, (-1, 1.6), color='steelblue')
sage: p = graphics_array([pF, pG, pF + pG])
sage: p.show(figsize=(7, 3))
Launched png viewer for Graphics Array of size 1 x 3
