Revision history [back]
 | 1 | initial version |
Given a function $f:\mathbb{C}\to\mathbb{C}$, the objective is to plot the set $$R=\{z\in\mathbb{C} \mid f(z)\in[0,1]\},$$ or, equivalently, $$S=\{(x,y)\in\mathbb{R}^2 \mid 0\leq P(x,y) \leq 1, \ Q(x,y)=0\},$$ where $P(x,y)$ and $Q(x,y)$ are, repectively, the real and the imaginary parts of $f(x+ i\,y)$.
In the approach followed in the OP, the bottleneck is the evaluation of the symbolic expression F, which is equal to $f(x+i\,y)$. To speed up computations, we can use the function fast_callable in order to transform F into a bivariate function that can be quickly evaluated:
var("x,y,z")
num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3)
den = (2*z-3)*(z-2)^3*z
f = num/den
F = fast_callable(f.subs(z == x + I*y), vars=[x,y], domain=CDF)
Now F behaves as a bivariate function which yields complex numbers, using floating point arithmetic. For example,
sage: F(1,2)
-2.8235294117647056 + 4.705882352941177*I
We next define P and Q, and plot the set $S$:
P = lambda x, y: F(x,y).real()
Q = lambda x, y: F(x,y).imag()
threshold = 5e-3
S = lambda x, y: 0 <= P(x,y) <= 1 and abs(Q(x,y)) < threshold
pS = region_plot(S, (x, 0, 5), (y, -1, 1), plot_points=501,
incol="lightgreen", bordercol="darkgreen")
show(pS, frame=True, axes=False)
The result is

Observe that, since we are using floating point arithmetic, a condition like Q(x,y)==0 does not work, due to rounding errors. So we have replaced it by abs(Q(x,y)) < threshold. Likewise, a large number of plot points is required to get a visually smooth region. Even so, the image is not satisfactory, so let us explore a different approach.
Instead of region_plot, we now use contour_plot and implicit_plot to draw, respectively, the region associated to the constraint $0\leq P(x,y)\leq 1$ and the curve $Q(x,y)=0$. Then we superimpose both plots:
pP = contour_plot(P, (0, 5), (-1, 1), contours=[0,1],
plot_points=101, cmap=["white","green","white"])
pQ = implicit_plot(Q, (0, 5), (-1, 1), color="red")
show(pP+pQ)
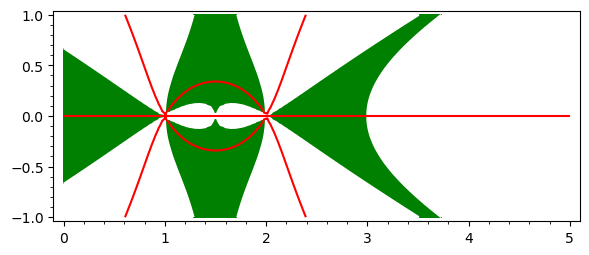
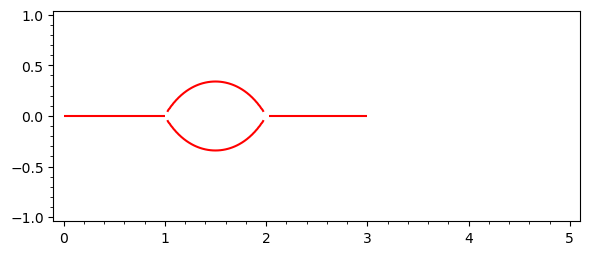
Hence $S$ is the set of red lines on the green background, quite similar, by the way, to the set shown in the first picture. Can we isolate those red lines? Yes, by using the region option:
implicit_plot(Q, (0, 5), (-1, 1), region=lambda x,y: 0<= P(x,y) <= 1,
plot_points=201, color="red")
Up to now we have dealt with the first function $f$ given in the OP. For the second one, it suffices to change num and den as follows:
num = -(z^8 -16*z^7+108*z^6-400*z^5+886*z^4-1200*z^3+972*z^2-432*z+81)*(z-2)^6*(z-4)*z
den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
And then repeat all the steps. We get the following pictures:

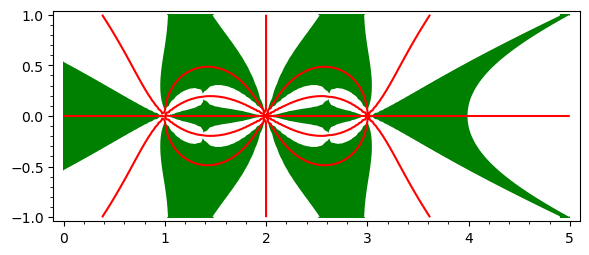
The complete code for the second case can be seen in this SageMathCell.
 | 2 | No.2 Revision |
Given a function $f:\mathbb{C}\to\mathbb{C}$, the objective is to plot the set $$R=\{z\in\mathbb{C} \mid f(z)\in[0,1]\},$$ or, equivalently, $$S=\{(x,y)\in\mathbb{R}^2 \mid 0\leq P(x,y) \leq 1, \ Q(x,y)=0\},$$ where $P(x,y)$ and $Q(x,y)$ are, repectively, the real and the imaginary parts of $f(x+ i\,y)$.
In the approach followed in the OP, original post, the bottleneck is the evaluation evaluation
of the symbolic expression F, which is equal to $f(x+i\,y)$. To speed up up
computations, we can use the function fast_callable in order to to
transform F into a bivariate function that can be quickly evaluated:
var("x,y,z")
num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3)
den = (2*z-3)*(z-2)^3*z
f = num/den
F = fast_callable(f.subs(z == x + I*y), vars=[x,y], domain=CDF)
Now F behaves as a bivariate function which yields complex numbers, numbers,
using floating point arithmetic. For example,
sage: F(1,2)
-2.8235294117647056 + 4.705882352941177*I
We next define P and Q, and plot the set $S$:
P = lambda x, y: F(x,y).real()
Q = lambda x, y: F(x,y).imag()
threshold = 5e-3
S = lambda x, y: 0 <= P(x,y) <= 1 and abs(Q(x,y)) < threshold
pS = region_plot(S, (x, 0, 5), (y, -1, 1), plot_points=501,
incol="lightgreen", bordercol="darkgreen")
show(pS, frame=True, axes=False)
The result is


Observe that, since we are using floating point arithmetic, a condition condition
like Q(x,y)==0 does not work, due to rounding errors. So we have replaced it it
by abs(Q(x,y)) < threshold. Likewise, a large number of plot points is required required
to get a visually smooth region. Even so, the image is not satisfactory, satisfactory,
so let us explore a different approach.
Instead of region_plot, we now use contour_plot and implicit_plot to draw, draw,
respectively, the region associated to the constraint $0\leq P(x,y)\leq 1$ and the the
curve $Q(x,y)=0$. Then we superimpose both plots:
pP = contour_plot(P, (0, 5), (-1, 1), contours=[0,1],
plot_points=101, cmap=["white","green","white"])
pQ = implicit_plot(Q, (0, 5), (-1, 1), color="red")
show(pP+pQ)


Hence $S$ is the set of red lines on the green background, quite similar, by the way, to the set shown in the first picture. Can we isolate those red lines? Yes, by using the region option:
implicit_plot(Q, (0, 5), (-1, 1), region=lambda x,y: 0<= P(x,y) <= 1,
plot_points=201, color="red")


Up to now we have dealt with the first function $f$ given in the OP. For the second one, it suffices to change num and den as follows:
num = -(z^8 -16*z^7+108*z^6-400*z^5+886*z^4-1200*z^3+972*z^2-432*z+81)*(z-2)^6*(z-4)*z
den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
And then repeat all the steps. We get the following pictures:






The complete code for the second case can be seen in this SageMathCell.
The above code for "implicit plot of Im = 0 in the region 0 <= Re <= 1" as a function:
def pre01_line(f, xx=(0, 4), yy=(-1, 1), **opt):
r"""
Return the preimage of the unit interval under this map.
INPUT:
- ``f`` -- a complex map as a symbolic expression
- ``xx``, ``yy`` -- the range of ``x`` and ``yy`` where to plot
"""
z = f.variables()[0]
x, y = SR.var('x, y')
F = fast_callable(f.subs({z: x + I*y}), vars=[x, y], domain=CDF)
P = lambda x, y: F(x, y).real()
Q = lambda x, y: F(x, y).imag()
op = {'region': lambda x, y: 0 <= P(x, y) <= 1,
'plot_points': 129, 'color': 'red'}
for k, v in op.items():
if k not in opt:
opt[k] = v
p = implicit_plot(Q, xx, yy, **opt)
return p
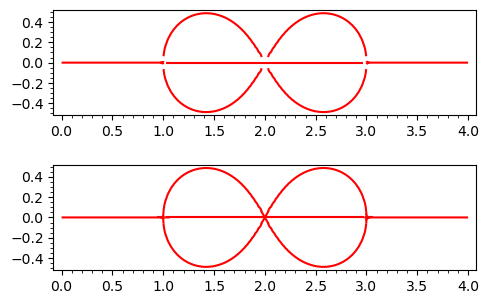
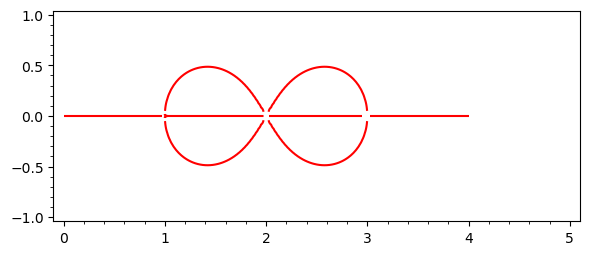
Lines don't quite meet in some places (a tighter bounding box improves things though):
num = -(z^8 -16*z^7+108*z^6-400*z^5+886*z^4-1200*z^3+972*z^2-432*z+81)*(z-2)^6*(z-4)*z
den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
f = num/den
a = pre01_line(f, xx=(0, 4), yy=(-0.5, 0.5))
a.show()
Increasing the number of plot points on the whole figure would be computationally wasteful.
Instead, why not simply fill in the small missing patches:
b = sum((pre01_line(f, xx=(k - eps, k + eps), yy=(-eps, eps), plot_points=65)
for k in (1, 2, 3) for eps in [1/16]), a)
b.show()
Compare the two plots:
ab = graphics_array([a, b], ncols=1)
ab.show(transparent=True, figsize=5)