Ask Your Question

Revision history [back]

click to hide/show revision 1
initial version

answered 2020-12-21 10:57:45 +0200

FrédéricC gravatar image

Are you working on dessins d'enfants ?

Here is a simple idea for an approximate plot

sage: x = polygen(QQ, 'x')                                           
sage: f = 1/729*(2*x**2-3*x+9)**3*(x+1)                           
sage: N = 50               
sage: sum(point2d(root) for k in range(N+1) for root in (f - k / N).complex_roots())
click to hide/show revision 2
No.2 Revision

updated 2020-12-23 19:11:35 +0200

slelievre gravatar image

Are you working on dessins d'enfants ?d'enfants?

Here is a simple idea for an approximate plotplot.

sage: x = polygen(QQ, 'x')                                           
sage: f = 1/729*(2*x**2-3*x+9)**3*(x+1)                           
sage: N = 50               
sage: sum(point2d(root) point2d(root for k in range(N+1) for root in (f - k / N).complex_roots())

The function pre01 below builds on this idea.

It gives a good idea of the desired plot and runs very fast.

def pre01(f, n=50, **opt):
    r"""
    Return the preimage of the unit interval under this rational function.

    INPUT:

    - ``f`` -- a rational function

    - ``n`` -- optional (default: 50) -- roughly how many points
      in the unit interval [0, 1] to use for preparing the plot

    Roughly a third or the points are inverse powers of two,
    roughly a third are one minus inverse powers of two,
    and roughly a third are linearly spaced along the interval.

    EXAMPLES::

        sage: x = polygen(QQ, 'x')
        sage: f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
        sage: pre01(f, n=50, color='teal').show(figsize=5)

        sage: z = polygen(QQ, 'z')
        sage: num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
        sage: den = (2*z-3)*(z-2)^3*z
        sage: pre01(num/den, n=50, color='steelblue').show(figsize=7)

        sage: Qz.<z> = QQ[]
        sage: cc = [81, -432, 972, -1200, 886, -400, 108, -16, 1]
        sage: num = -Qz(cc)*(z-2)^6*(z-4)*z
        sage: den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
        sage: pre01(num/den, n=50, color='firebrick').show(figsize=7)
    """
    nn = n // 3 + 2
    num, den = f.numerator(), f.denominator()
    tt = [0] + [ZZ(2)**-k for k in (0 .. nn)]
    tt.extend([1 - t for t in tt[3:]])
    tt.extend(QQ((k, nn)) for k in (1 .. nn - 1))
    zz = (root for t in set(tt) for root in (num - t*den).complex_roots())
    cols = {'color': 'teal', 'axes_color': 'grey',
            'axes_label_color': 'grey', 'tick_label_color': 'grey'}
    op = {'size': 4, 'color': 'teal', 'zorder': 3, 'aspect_ratio': 1}
    for k, v in opt.items():
        if 'color' in k:
            cols[k] = v
        else
            op[k] = v
    G = point2d(zz, color=cols['color'] **op)
    G.axes_color(cols['axes_color'])
    G.axes_label_color(cols['axes_label_color'])
    G.tick_label_color(cols['tick_label_color'])
    return G

Three examples of usage.

Our quick example from above:

x = polygen(QQ, 'x')
f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
p = pre01(f, n=50, color='teal')
p.show(figsize=5)

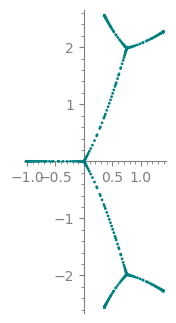
Preimage of unit interval under map f

The first example in the question:

z = polygen(QQ, 'z')
num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
den = (2*z-3)*(z-2)^3*z
p = pre01(num/den, n=50, color='steelblue')
p.show(figsize=5)

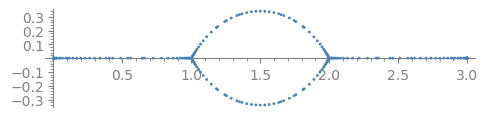
Preimage of unit interval under first map in question

The second example in the question:

z = polygen(QQ, 'z')
num = -(z^8-16*z^7+108*z^6-400*z^5+886*z^4-1200*z^3+972*z^2-432*z+81)*(z-2)^6*(z-4)*z
den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
p = pre01(num/den, n=50, color='firebrick')
p.show(figsize=5)

Preimage of unit interval under second map in question

Each of those three examples runs in under a second.
click to hide/show revision 3
No.3 Revision

updated 2020-12-23 19:22:25 +0200

slelievre gravatar image

Are you working on dessins d'enfants?

Here is a simple idea for an approximate plot.

sage: x = polygen(QQ, 'x')                                           
sage: f = 1/729*(2*x**2-3*x+9)**3*(x+1)                           
sage: N = 50               
sage: point2d(root for k in range(N+1) for root in (f - k / N).complex_roots())

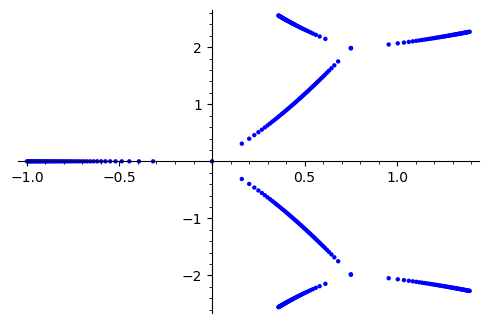
Quick example: preimage of unit interval under rational function

The function pre01 below builds on this idea.

idea. It gives a good idea of the desired plot and runs very fast.

def pre01(f, n=50, **opt):
    r"""
    Return the preimage of the unit interval under this rational function.

    INPUT:

    - ``f`` -- a rational function

    - ``n`` -- optional (default: 50) -- roughly how many points
      in the unit interval [0, 1] to use for preparing the plot

    Roughly a third or the points are inverse powers of two,
    roughly a third are one minus inverse powers of two,
    and roughly a third are linearly spaced along the interval.

    EXAMPLES::

        sage: x = polygen(QQ, 'x')
        sage: f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
        sage: pre01(f, n=50, color='teal').show(figsize=5)

        sage: z = polygen(QQ, 'z')
        sage: num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
        sage: den = (2*z-3)*(z-2)^3*z
        sage: pre01(num/den, n=50, color='steelblue').show(figsize=7)
color='steelblue').show(figsize=5)

        sage: Qz.<z> = QQ[]
        sage: cc = [81, -432, 972, -1200, 886, -400, 108, -16, 1]
        sage: num = -Qz(cc)*(z-2)^6*(z-4)*z
        sage: den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
        sage: pre01(num/den, n=50, color='firebrick').show(figsize=7)
color='firebrick').show(figsize=5)
    """
    nn = n // 3 + 2
    num, den = f.numerator(), f.denominator()
    tt = [0] + [ZZ(2)**-k for k in (0 .. nn)]
    tt.extend([1 - t for t in tt[3:]])
    tt.extend(QQ((k, nn)) for k in (1 .. nn - 1))
    zz = (root for t in set(tt) for root in (num - t*den).complex_roots())
    cols = {'color': 'teal', 'axes_color': 'grey',
            'axes_label_color': 'grey', 'tick_label_color': 'grey'}
    op = {'size': 4, 'color': 'teal', 'zorder': 3, 'aspect_ratio': 1}
    for k, v in opt.items():
        if 'color' in k:
            cols[k] = v
        else
else:
            op[k] = v
    G = point2d(zz, color=cols['color'] **op)
    G.axes_color(cols['axes_color'])
    G.axes_label_color(cols['axes_label_color'])
    G.tick_label_color(cols['tick_label_color'])
    return G

Three examples of usage.using this function follow.

Our quick example from above:

x = polygen(QQ, 'x')
f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
p = pre01(f, n=50, color='teal')
p.show(figsize=5)

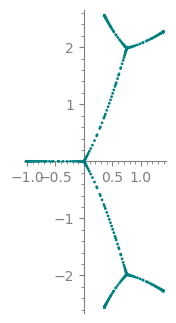
Preimage of unit interval under map f

The first example in the question:

z = polygen(QQ, 'z')
num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
den = (2*z-3)*(z-2)^3*z
p = pre01(num/den, n=50, color='steelblue')
p.show(figsize=5)

Preimage of unit interval under first map in question

The second example in the question:

z = polygen(QQ, 'z')
num = -(z^8-16*z^7+108*z^6-400*z^5+886*z^4-1200*z^3+972*z^2-432*z+81)*(z-2)^6*(z-4)*z
den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
p = pre01(num/den, n=50, color='firebrick')
p.show(figsize=5)

Preimage of unit interval under second map in question

Each of those three examples runs in under a second.

Are you working on dessins d'enfants?

Here is a simple idea for an approximate plot.

sage: x = polygen(QQ, 'x')                                           
sage: f = 1/729*(2*x**2-3*x+9)**3*(x+1)                           
sage: N = 50               
sage: point2d(root for k in range(N+1) for root in (f - k / N).complex_roots())

Quick example: preimage of unit interval under rational function

The function pre01 below builds on this idea. It gives a good idea of the desired plot and runs fast.

def pre01(f, n=50, **opt):
    r"""
    Return the preimage of the unit interval under this rational function.

    INPUT:

    - ``f`` -- a rational function

    - ``n`` -- optional (default: 50) -- roughly how many points
      in the unit interval [0, 1] to use for preparing the plot

    Roughly a third or the points are inverse powers of two,
    roughly a third are one minus inverse powers of two,
    and roughly a third are linearly spaced along the interval.

    EXAMPLES::

        sage: x = polygen(QQ, 'x')
        sage: f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
        sage: pre01(f, n=50, color='teal').show(figsize=5)

        sage: z = polygen(QQ, 'z')
        sage: num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
        sage: den = (2*z-3)*(z-2)^3*z
        sage: pre01(num/den, n=50, color='steelblue').show(figsize=5)

        sage: Qz.<z> = QQ[]
        sage: cc = [81, -432, 972, -1200, 886, -400, 108, -16, 1]
        sage: num = -Qz(cc)*(z-2)^6*(z-4)*z
        sage: den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
        sage: pre01(num/den, n=50, color='firebrick').show(figsize=5)
    """
    nn = n // 3 + 2
    num, den = f.numerator(), f.denominator()
    tt = [0] + [ZZ(2)**-k for k in (0 .. nn)]
    tt.extend([1 - t for t in tt[3:]])
    tt.extend(QQ((k, nn)) for k in (1 .. nn - 1))
    zz = (root for t in set(tt) for root in (num - t*den).complex_roots())
    cols = {'color': 'teal', 'axes_color': 'grey',
            'axes_label_color': 'grey', 'tick_label_color': 'grey'}
    op = {'size': 4, 'color': 'teal', 'zorder': 3, 'aspect_ratio': 1}
    for k, v in opt.items():
        if 'color' in k:
            cols[k] = v
        else:
            op[k] = v
    G = point2d(zz, color=cols['color'] color=cols['color'], **op)
    G.axes_color(cols['axes_color'])
    G.axes_label_color(cols['axes_label_color'])
    G.tick_label_color(cols['tick_label_color'])
    return G

Three examples of using this function follow.

Our quick example from above:

x = polygen(QQ, 'x')
f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
p = pre01(f, n=50, color='teal')
p.show(figsize=5)

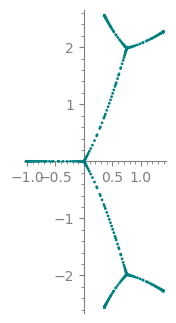
Preimage of unit interval under map f

The first example in the question:

z = polygen(QQ, 'z')
num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
den = (2*z-3)*(z-2)^3*z
p = pre01(num/den, n=50, color='steelblue')
p.show(figsize=5)

Preimage of unit interval under first map in question

The second example in the question:

z = polygen(QQ, 'z')
num = -(z^8-16*z^7+108*z^6-400*z^5+886*z^4-1200*z^3+972*z^2-432*z+81)*(z-2)^6*(z-4)*z
den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
p = pre01(num/den, n=50, color='firebrick')
p.show(figsize=5)

Preimage of unit interval under second map in question

Each of those three examples runs in under a second.

click to hide/show revision 5
No.5 Revision

updated 2020-12-23 23:40:49 +0200

slelievre gravatar image

Are you working on dessins d'enfants?

Here is a simple idea for an approximate plot.

sage: x = polygen(QQ, 'x')                                           
sage: f = 1/729*(2*x**2-3*x+9)**3*(x+1)                           
sage: N = 50               
sage: point2d(root for k in range(N+1) for root in (f - k / N).complex_roots())

Quick example: preimage of unit interval under rational function

The function pre01 below builds on this idea. It gives a good idea of the desired plot and runs fast.

def pre01(f, n=50, style='dots', **opt):
    r"""
    Return the preimage of the unit interval under this rational function.

    INPUT:

    - ``f`` -- a rational function

    - ``n`` -- optional (default: 50) -- roughly how many points
      in the unit interval [0, 1] to use for preparing the plot

    Roughly a third or the points are inverse powers of two,
    roughly a third are one minus inverse powers of two,
    and roughly a third are linearly spaced along the interval.

    EXAMPLES::

        sage: x = polygen(QQ, 'x')
        sage: f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
        sage: pre01(f, n=50, color='teal').show(figsize=5)
style='dots', color='firebrick').show(figsize=5)
        sage: pre01(f, n=50, style='line', color='firebrick').show(figsize=5)

        sage: z = polygen(QQ, 'z')
        sage: num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
        sage: den = (2*z-3)*(z-2)^3*z
        sage: pre01(num/den, g = num/den
        sage: pre01(g, n=50, color='steelblue').show(figsize=5)
style='dots', color='firebrick').show(figsize=5)
        sage: pre01(g, n=50, style='line', color='firebrick').show(figsize=5)

        sage: Qz.<z> = QQ[]
        sage: cc = [81, -432, 972, -1200, 886, -400, 108, -16, 1]
        sage: num = -Qz(cc)*(z-2)^6*(z-4)*z
        sage: den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
        sage: pre01(num/den, h = num/den
        sage: pre01(h, n=50, style='dots', color='firebrick').show(figsize=5)
        sage: pre01(h, n=50, style='line', color='firebrick').show(figsize=5)
    """
    nn = n // 3 + 2
    num, den = f.numerator(), f.denominator()
    tt = [0] + [ZZ(2)**-k for k in (0 .. nn)]
    tt.extend([1 - t for t in tt[3:]])
    tt.extend(QQ((k, nn)) for k in (1 .. nn - 1))
    zz = (root for t in set(tt) for root in (num - t*den).complex_roots())
tt = sorted(set(tt))
    cols = {'color': 'teal', 'axes': True, 'axes_color': 'grey',
            'axes_label_color': 'grey', 'tick_label_color': 'grey'}
    op = {'size': dop = {'aspect_ratio': 1, 'size': 4, 'color': 'teal', 'zorder': 3, 'aspect_ratio': 1}
10}
    lop = {'aspect_ratio': 1, 'edge_thickness': 2}
    for k, v in opt.items():
        if 'color' in k or 'axis' in k or 'axes' in k or 'tick' in k:
            cols[k] = v
        elif k == 'size':
            dop[k] = v
        elif k == 'edge_thickness':
            lop[k] = v
        else:
            op[k] dop[k] = lop[k] = v
    if style == 'dots':
        zz = (root for t in set(tt) for root in (num - t*den).complex_roots())
        G = point2d(zz, color=cols['color'], **op)
**dop)
    elif style == 'line':
        tzz = {t: (num - t*den).complex_roots() for t in tt}
        D = Graph()
        for k, t in enumerate(tt[1:-1], start=1):
            s, u = tt[k-1], tt[k+1]
            szz, uzz = tzz[s], tzz[u]
            for z in tzz[t]:
                zs = min((abs(z - w), w) for w in szz)[1]
                D.add_edge(z, zs, k-1)
                zu = min((abs(z - w), w) for w in uzz)[1]
                D.add_edge(z, zu, k)
        D.set_pos({z: (z.real(), z.imag()) for z in D})
        ecol = {cols['color']: D.edges()}
        G = D.plot(vertex_labels=False, vertex_size=0, edge_colors=ecol, **lop)
    else:
        raise ValueError(f"style should be 'dots' or 'line', got :'{style}'")
    G.axes(cols['axes'])
    G.axes_color(cols['axes_color'])
    G.axes_label_color(cols['axes_label_color'])
    G.tick_label_color(cols['tick_label_color'])
    return G

Three examples of using this function follow.

Our quick Quick starting example from above:of this answer:

x = polygen(QQ, 'x')
f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
p a_dots = pre01(f, n=50, style='dots, color='teal')
p.show(figsize=5)
a_line = pre01(f, n=50, style='line', color='teal')
a_dots_lines = graphics_array([a_dots, a_line], ncols=2)
a_dots_lines.show(figsize=5)

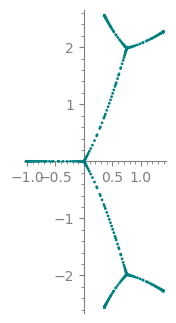
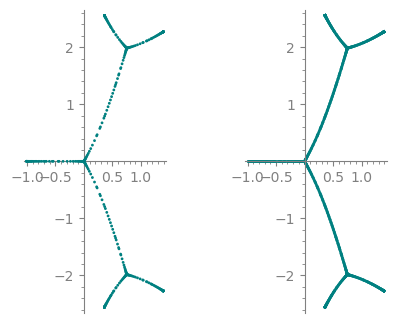
Preimage of unit interval under map fPreimage of unit interval under map f

The first First example in the question:

z = polygen(QQ, 'z')
num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
den = (2*z-3)*(z-2)^3*z
p b_dots = pre01(num/den, n=50, style='dots', color='steelblue')
p.show(figsize=5)
b_line = pre01(num/den, n=50, style='line', color='steelblue')
b_dots_lines = graphics_array([b_dots, b_line], ncols=1)
b_dots_lines.show(figsize=5)

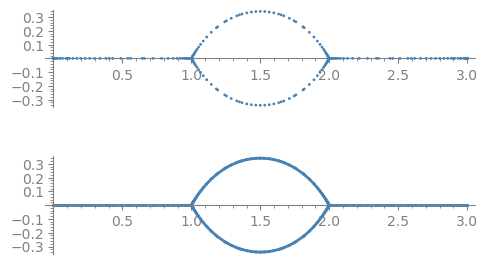
Preimage of unit interval under first map in questionPreimage of unit interval under first map in question

The second Second example in the question:

z = polygen(QQ, 'z')
num = -(z^8-16*z^7+108*z^6-400*z^5+886*z^4-1200*z^3+972*z^2-432*z+81)*(z-2)^6*(z-4)*z
den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
p c_dots = pre01(num/den, n=50, style='dots', color='firebrick')
p.show(figsize=5)
c_line = pre01(num/den, n=50, style='line', color='firebrick')
c_dots_lines = graphics_array([c_dots, c_line], ncols=1)
c_dots_lines.show(figsize=5)

Preimage of unit interval under second map in questionPreimage of unit interval under second map in question

Each of those three examples runs in under a second.second per plot style.

Are you working on dessins d'enfants?

Here is a simple idea for an approximate plot.

sage: x = polygen(QQ, 'x')                                           
sage: f = 1/729*(2*x**2-3*x+9)**3*(x+1)                           
sage: N = 50               
sage: point2d(root for k in range(N+1) for root in (f - k / N).complex_roots())

Quick example: preimage of unit interval under rational function

The function pre01 below builds on this idea. It gives a good idea of the desired plot and runs fast.

def pre01(f, n=50, style='dots', **opt):
    r"""
    Return the preimage of the unit interval under this rational function.

    INPUT:

    - ``f`` -- a rational function

    - ``n`` -- optional (default: 50) -- roughly how many points
      in the unit interval [0, 1] to use for preparing the plot

    Roughly a third or the points are inverse powers of two,
    roughly a third are one minus inverse powers of two,
    and roughly a third are linearly spaced along the interval.

    EXAMPLES::

        sage: x = polygen(QQ, 'x')
        sage: f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
        sage: pre01(f, n=50, style='dots', color='firebrick').show(figsize=5)
        sage: pre01(f, n=50, style='line', color='firebrick').show(figsize=5)

        sage: z = polygen(QQ, 'z')
        sage: num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
        sage: den = (2*z-3)*(z-2)^3*z
        sage: g = num/den
        sage: pre01(g, n=50, style='dots', color='firebrick').show(figsize=5)
        sage: pre01(g, n=50, style='line', color='firebrick').show(figsize=5)

        sage: Qz.<z> = QQ[]
        sage: cc = [81, -432, 972, -1200, 886, -400, 108, -16, 1]
        sage: num = -Qz(cc)*(z-2)^6*(z-4)*z
        sage: den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
        sage: h = num/den
        sage: pre01(h, n=50, style='dots', color='firebrick').show(figsize=5)
        sage: pre01(h, n=50, style='line', color='firebrick').show(figsize=5)
    """
    nn = n // 3 + 2
    num, den = f.numerator(), f.denominator()
    tt = [0] + [ZZ(2)**-k for k in (0 .. nn)]
    tt.extend([1 - t for t in tt[3:]])
    tt.extend(QQ((k, nn)) for k in (1 .. nn - 1))
    tt = sorted(set(tt))
    cols = {'color': 'teal', 'axes': True, 'axes_color': 'grey',
            'axes_label_color': 'grey', 'tick_label_color': 'grey'}
    dop = {'aspect_ratio': 1, 'size': 4, 'zorder': 10}
    lop = {'aspect_ratio': 1, 'edge_thickness': 2}
    for k, v in opt.items():
        if 'color' in k or 'axis' in k or 'axes' in k or 'tick' in k:
            cols[k] = v
        elif k == 'size':
            dop[k] = v
        elif k == 'edge_thickness':
            lop[k] = v
        else:
            dop[k] = lop[k] = v
    if style == 'dots':
        zz = (root for t in set(tt) for root in (num - t*den).complex_roots())
        G = point2d(zz, color=cols['color'], **dop)
    elif style == 'line':
        tzz = {t: (num - t*den).complex_roots() for t in tt}
        D = Graph()
        for k, t in enumerate(tt[1:-1], start=1):
            s, u = tt[k-1], tt[k+1]
            szz, uzz = tzz[s], tzz[u]
            for z in tzz[t]:
                zs = min((abs(z - w), w) for w in szz)[1]
                D.add_edge(z, zs, k-1)
                zu = min((abs(z - w), w) for w in uzz)[1]
                D.add_edge(z, zu, k)
        D.set_pos({z: (z.real(), z.imag()) for z in D})
        ecol = {cols['color']: D.edges()}
        G = D.plot(vertex_labels=False, vertex_size=0, edge_colors=ecol, **lop)
    else:
        raise ValueError(f"style should be 'dots' or 'line', got :'{style}'")
    G.axes(cols['axes'])
    G.axes_color(cols['axes_color'])
    G.axes_label_color(cols['axes_label_color'])
    G.tick_label_color(cols['tick_label_color'])
    return G

Three examples of using this function follow.

Quick starting example of this answer:

x = polygen(QQ, 'x')
f = 1/729 * (2 * x**2 - 3 * x + 9)**3 * (x + 1)
a_dots = pre01(f, n=50, style='dots, style='dots', color='teal')
a_line = pre01(f, n=50, style='line', color='teal')
a_dots_lines = graphics_array([a_dots, a_line], ncols=2)
a_dots_lines.show(figsize=5)

Preimage of unit interval under map f

First example in the question:

z = polygen(QQ, 'z')
num = -(z^4-6*z^3+12*z^2-8*z)*(z-1)^3*(z-3) 
den = (2*z-3)*(z-2)^3*z
b_dots = pre01(num/den, n=50, style='dots', color='steelblue')
b_line = pre01(num/den, n=50, style='line', color='steelblue')
b_dots_lines = graphics_array([b_dots, b_line], ncols=1)
b_dots_lines.show(figsize=5)

Preimage of unit interval under first map in question

Second example in the question:

z = polygen(QQ, 'z')
num = -(z^8-16*z^7+108*z^6-400*z^5+886*z^4-1200*z^3+972*z^2-432*z+81)*(z-2)^6*(z-4)*z
den = (6*z^4-48*z^3+140*z^2-176*z+81)*(z-1)^4*(z-3)^4
c_dots = pre01(num/den, n=50, style='dots', color='firebrick')
c_line = pre01(num/den, n=50, style='line', color='firebrick')
c_dots_lines = graphics_array([c_dots, c_line], ncols=1)
c_dots_lines.show(figsize=5)

Preimage of unit interval under second map in question

Each of those three examples runs in under a second per plot style.

Copyright Sage, 2010. Some rights reserved under creative commons license. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.
about | faq | help | privacy policy | terms of service
Powered by Askbot version 0.7.59