Revision history [back]

Hello, @aylimenz! This is a very deep question or an easy question, depending on what you are trying to learn from these words. Although I am not entitled to clarify exactly what the authors mean to convey with the text you cited, I can give you some points of view based on my personal experience. I will assume you (or anyone reading this answer) is a beginner, so this will be a long text.

The descriptions "too complex" and "not having an explicit solution" are not specific terms in this context; they are more like intuitive concepts. Basically, an equation has no explicit solution whenever Sage is unable to find a symbolic solution. For example, in this particular case, you can see that Sage has returned the equation itself, which basically is an admission of defeat. With that in mind, an equation is too complex is Sage cannot find an explicit solution.
But there exists another way of understanding "too complex." Consider the relative complexity of the equation in your question, compared to a polynomial equation. From the point of view of a human, this particular equation is more difficult to visualize/analyze/understand/solve. From this point of view, "too complex" can be understood as "too complicated," "too exotic," "way too elaborated," "too strange," "too uncommon." With practice, you will learn to recognize this kind of problems just by sight.
The previous point doesn't mean that Sage in incapable of solving equations more complicated than a polynomial; on the contrary, it can in fact solve extremely complicated equations and system. However, the more exotic your equation is, the more probable is that symbolic algorithm fail to solve it. As an example, consider a fifth-degree polynomial (for which I hope you know there is no explicit formula), inside an absolute, elevated to the sine of a third degree polynomial:

$$|3x^5 + 2x^4 - 5x^3 + 23x^2 - 15x - 56|^{\sin(63x^3-5x^2+3)}=0.$$

Although this is an extreme example, it clearly illustrates the point at hand ("too complex"). I believe you will agree that we cannot expect Sage or any other current software to give a meaningful symbolic solution to this one.
When Symbolic algorithms fall short, there are some things you can still try. For example, in the case of the equation on your question, you can try to find a numerical solution, as @Emmanuel Charpentier suggests. The find_root() function takes an equation and the extremes of an interval to search the solution as input arguments. In this case, you can try:
```
find_root(x^(1/x)==(1/x)^x, 0, 2)
```
in order to find a root in the interval $(0,2)$. This will be an approximation (or exact solution if you are lucky), but it is way better than the output of solve(). The interval to find the solution doesn't have to be a very good guess; you can try something more gross, like
```
find_root(x^(1/x)==(1/x)^x, 0, 10^4)
```
(Of course, the worse the interval guess, the harder for the algorithm to find the solution.) It is always a good idea to plot the functions to have a good idea of the interval:
```
p = plot(x^(1/x), 0, 5)
p += plot((1/x)^x, 0, 5)
p.show()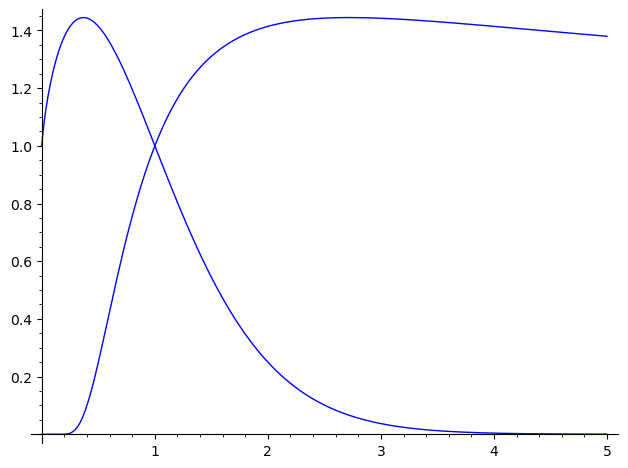
```
How do you know if that is the only solution? Why did I used the interval $[0,5]$ to plot? What else can you do in order to obtain additional information about this equation? You should use a combination of mathematical analysis and intuition in order to go further. Of course, Sage can help you with the part of mathematical analysis (by finding derivatives, by plotting functions, etc.), but the intuition is best developed through experience.
As the authors of the book indicate, when a too complex equation is presented, it is generally the case that the equation has a deeper meaning than the solution itself (hence the complexity). So being unable to find an explicit solution is not a problem, because you can do more profound and productive things with that equation than obtaining a simple solution. As in the previous point, obtaining meaningful information and studying the general behavior of a mathematical expression consists basically on doing some mathematical analysis, which Sage can help you with.

I hope this helps!