Revision history [back]

Your plot :

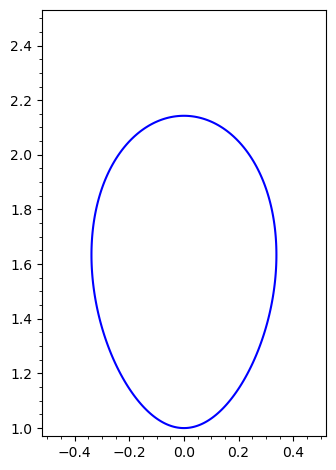
hints that for x=1/5, there may be two possible values of y satisfying g : one almost surely between 1 and 3/2, the other almost surely between 3/2 and 11/5.

We may seek numerical roots of the left-hand side of g:

sage: (g.rhs()-g.lhs()).subs(x=1/5).find_root(1,3/2)
1.1442861670756799
sage: (g.rhs()-g.lhs()).subs(x=1/5).find_root(3/2,11/5)
2.0490321780635146

Finding symbolic solutions is harder. Most algorithms available to sage fail miserably :

sage: solve(g.subs(x==1/5),y)
[sqrt(25*y^2 - 100*y + 101) == -3/4*sqrt(25*y^2 + 1) + 35/4]
sage: solve(g.subs(x==1/5),y, to_poly_solve=True)
[]
sage: solve(g.subs(x==1/5),y, algorithm="fricas")
[sqrt(25*y^2 - 100*y + 101) == -3/4*sqrt(25*y^2 + 1) + 35/4]
sage: solve(g.subs(x==1/5),y, algorithm="giac")
[sqrt(25*y^2 - 100*y + 101) == -3/4*sqrt(25*y^2 + 1) + 35/4]

However, sympy is able to find a solution :

[[y == -1/1225*sqrt(2)*sqrt(1500625*(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 1432516/(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 9182600) + sqrt(-2*(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) - 50400*sqrt(2)/sqrt(1500625*(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 1432516/(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 9182600) - 2865032/1500625/(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 29984/1225) + 32/7,
  y == 1/1225*sqrt(2)*sqrt(1500625*(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 1432516/(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 9182600) - sqrt(-2*(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 50400*sqrt(2)/sqrt(1500625*(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 1432516/(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 9182600) - 2865032/1500625/(24/42875*I*sqrt(2776173) - 11970064/1838265625)^(1/3) + 29984/1225) + 32/7],
 ConditionSet(y, Eq(sqrt(25*y**2 + 1)/5 + 4*sqrt(25*(y - 2)**2 + 1)/15 - 7/3, 0), FiniteSet(32/7 + sqrt(29984/1225 - 2*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3) + 576/(7*sqrt(14992/1225 + 2865032/(1500625*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3)) + 2*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3))) - 2865032/(1500625*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3))) + sqrt(14992/1225 + 2865032/(1500625*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3)) + 2*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3)), 32/7 - sqrt(14992/1225 + 2865032/(1500625*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3)) + 2*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3)) - sqrt(29984/1225 - 2*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3) - 576/(7*sqrt(14992/1225 + 2865032/(1500625*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3)) + 2*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3))) - 2865032/(1500625*(-11970064/1838265625 + 24*sqrt(2776173)*I/42875)**(1/3)))))]

The second part of this solution (which is a sympy object, not yet translatable to sage, BTW) is a set of conditions. We shall ignore this for the moment...

The first part gives us two solutions, apparently complex. However, one can easily show formally that those roots are indeed real:

sage: [u.rhs().imag_part().is_zero() for u in Sol[0]]
[True, True]

Leaving the pleasure of finding a "nice" algebraic form of the real part of these roots to masochists, we can assess numerically the proximity of these answers to tjose obtained by numerical means:

sage: [u.rhs().real_part().n() for u in Sol[0]]
[1.14428616707569, 2.04903217806352]

We may also attempt a formal check :

sage: %time [g.lhs().subs(x==1/5).subs(y==s.rhs().real_part()).is_zero() for s in Sol[0]]

but this has no guarantee to even terminate and, anyway, exceeded my patience...

FWIW, "the competition" doesn't do much better :

sage: mathematica.Simplify(mathematica.Solve(g.subs(x==1/5),y))
{
 {y -> (-2*(-80 + Sqrt[3748 + 358129/(-1496258 + (128625*I)*Sqrt[2776173])^
          (1/3) + (-1496258 + (128625*I)*Sqrt[2776173])^(1/3)] - 
      Sqrt[7496 - 358129/(-1496258 + (128625*I)*Sqrt[2776173])^(1/3) - 
        (-1496258 + (128625*I)*Sqrt[2776173])^(1/3) - 
        441000/Sqrt[3748 + 358129/(-1496258 + (128625*I)*Sqrt[2776173])^
             (1/3) + (-1496258 + (128625*I)*Sqrt[2776173])^(1/3)]]))/35}, 
 {y -> (2*(80 + Sqrt[3748 + 358129/(-1496258 + (128625*I)*Sqrt[2776173])^
          (1/3) + (-1496258 + (128625*I)*Sqrt[2776173])^(1/3)] - 
      Sqrt[7496 - 358129/(-1496258 + (128625*I)*Sqrt[2776173])^(1/3) - 
        (-1496258 + (128625*I)*Sqrt[2776173])^(1/3) + 
        441000/Sqrt[3748 + 358129/(-1496258 + (128625*I)*Sqrt[2776173])^
             (1/3) + (-1496258 + (128625*I)*Sqrt[2776173])^(1/3)]]))/35}}
sage: mathematica.N(mathematica.Solve(g.subs(x==1/5),y))
{{y -> 1.1442861670756819 + 2.8197360586151467*^-16*I}, 
 {y -> 2.049032178063519 - 1.3904088425248892*^-16*I}}

HTH,