Revision history [back]

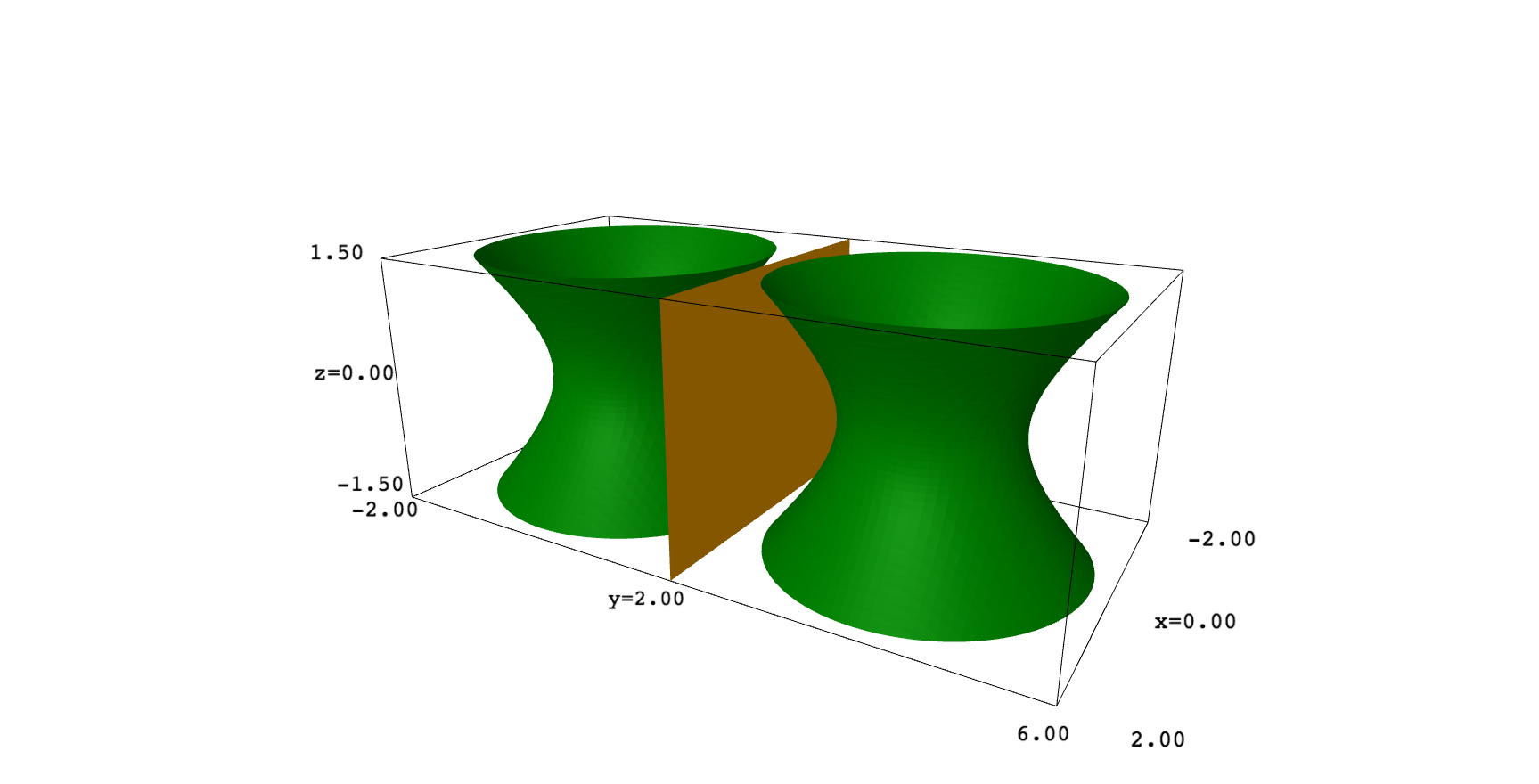
I don't understand what it is $R^{(-1,1)}$ and, IMHO, an hyperboloid is a surface, so it should be traced in 3D. In such a case, you can play with translations, scales and rotations to apply reflections. For example, this code plots a one sheet hyperboloid and mirrors it on the plane $y=2$:

var("x,y,z")
p = implicit_plot3d(x^2+y^2-z^2==1, (x,-2,2), (y,-2,2), (z,-1.5,1.5), color="green")
q = p.translate([0,-2,0]).scale([1,-1,1]).translate([0,2,0])
plane = implicit_plot3d(y==2,(x,-2,2), (y,-2,2), (z,-1.5,1.5), color="orange")
show(p+q+plane)