Revision history [back]

If you type

sage: d.simplify

and the tab key, you will see a pop-up frame showing different ways to complete that command to simplify d:

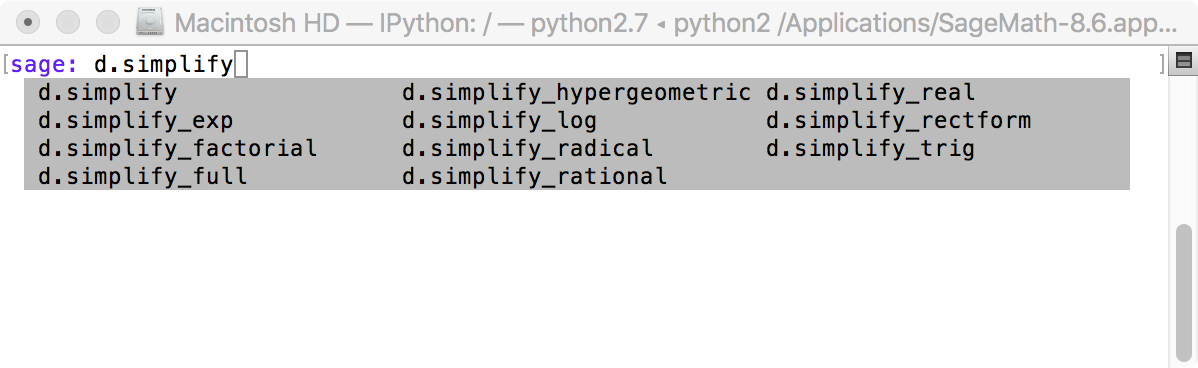
Select one of them, say simplify_full, and ? and press the return key to see the associated help:

sage: d.simplify_full?
Docstring:     
   Apply "simplify_factorial()", "simplify_rectform()",
   "simplify_trig()", "simplify_rational()", and then "expand_sum()"
   to self (in that order).

   ALIAS: "simplify_full" and "full_simplify" are the same.

   EXAMPLES:

      sage: f = sin(x)^2 + cos(x)^2
      sage: f.simplify_full()
      1

      sage: f = sin(x/(x^2 + x))
      sage: f.simplify_full()
      sin(1/(x + 1))
...........................

In this case, since d contains radicals, you may try another method:

sage: d.canonicalize_radical()

which is the actual form of the deprecated simplify_radical. Check if the resulting simplification is good enough for you.

If you type

sage: d.simplify

and the tab key, you will see a pop-up frame showing different ways to complete that command to simplify d:

Select one of them, say simplify_full, and add ? and press the return key to see the associated help:

sage: d.simplify_full?
Docstring:     
   Apply "simplify_factorial()", "simplify_rectform()",
   "simplify_trig()", "simplify_rational()", and then "expand_sum()"
   to self (in that order).

   ALIAS: "simplify_full" and "full_simplify" are the same.

   EXAMPLES:

      sage: f = sin(x)^2 + cos(x)^2
      sage: f.simplify_full()
      1

      sage: f = sin(x/(x^2 + x))
      sage: f.simplify_full()
      sin(1/(x + 1))
...........................

In this case, since d contains radicals, you may try another method:

sage: d.canonicalize_radical()

which is the actual form of the deprecated simplify_radical. Check if the resulting simplification is good enough for you.