Revision history [back]
 | 1 | initial version |
Okay. After 12 days, your (hypothetic) homework is past due. Let's look at a couple of solutions.
"when you're lost, draw what you know." Undergrads' wisdom. Let's see:
Without loss of generality, set up a framework placong the fence center in $O=(0,0)$ and the tether anchor in $A=(r_0,0)$. In this framework a point $(x,y)$ is edible by the goat if it is :
- inside the fence, implying $x^2+y^2<=r_0^2$, and
- closer to the tether's anchor than $r_1$, implying $(r-x)^2+y^2<=r1^2$.
In other words, the edible region is the intersection of two disks $D_0$, centered in $O$ with radius $r_0$ and $D_1$, centered in $A$ with radius $r_1$. This region can be exactly partitioned by the straight line segment joining the intersections of the two circles boundaries of these disks:
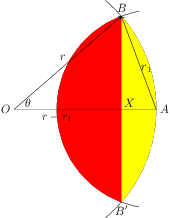
Each of these regions is the intersection of a disk of radius $r$ and a half-plane cutting the disk at a distance $X<=r$ of its center.
Therefore, a first, (almost) purely geometrical, solution to your problem is to derive the area of such a surface, and apply it to both the "yellow" and the "red" surfaces. Let's consider the "yellow" one, delimited bu th arc $B'AB$ and the straight segment $BB'$. This surface is symmetric about $OA$ ; therefore, its area is twice of the surface bounded by the arc $AB$ and the straight segments $BX$ and $XA$.
This latter surface can be in turn considered as the difference between
- the circular sector delimited by$OA$, $OB$, and
- the arc $AB$ and the triangle $BOX$.
Let's call $\theta$ the angle $\widehat{AOB}$. It can be determined from the position of $B$. We have of course $\cos\theta=\frac{OX}{r}=\frac{B_x}{r}$ and $\tan\theta={B_y}{B_x}$. At the high school level, this "determination" is a bit fuzzy, but will be clarified in first year of college...
The circular sector has area $\frac{r^2\theta}{2}$, the triangle has area $\frac{OX*XB}{2}=\frac{B_x B_y}{2}$. The yellow surface has area twice their difference, therefore $r_0^2 \theta - B_x\cdot B_y$.
For similar reasons (left to the reader as an exercise ; beware the signs !), with $\cos\theta_1=\frac{B_y}{r_1}$, the "red" sector has area $r_1^2\theta_1-(r_0-B_x) B_y$.
All that is lacking are the coordinates of $B$ which are determined by the fact that it belongs to both the boundary circles (the fence and the tether). Since there are two solution points, we'll select the one with positive ordinate :
x,y,r_0,r_1=var("x,y,r_0,r_1")
assume(x,"real",y,"real",r_0>0,r_1>0,r_1<2*r_0)
O=vector([0,0])
A=vector([r_0,0])
b=vector([x,y])
E0=(b-O).norm()^2==r_0^2
E1=(b-A).norm()^2==r_1^2
Sol=solve([E0, E1],[x,y], solution_dict=True)
if bool(Sol[0].get(y)>0):
B=vector([Sol[0].get(x),Sol[0].get(y)])
else:
B=vector([Sol[1].get(x),Sol[1].get(y)])
X=B[0]
Y=B[1]
That gives us $B=\left(\frac{2 \, r_{0}^{2} - r_{1}^{2}}{2 \, r_{0}},\ \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}}{2 \, r_{0}}\right)$.
This also determines the angle $\theta=\widehat{AOB}$ by either theta=arccos(X/r_0) or theta=arctan2(Y,X) (Note : the third "obvious" choice, theta=arcsin(Y./r_0 is unsuitable here, given the choice of branches of Sage's implementation of arcsin). We determine $\theta_1$ in a similar way (again, mind the signs...).
Summing the partial areas and finding the root (value of $r_1$ leaving an edible area of 10 when $r_0=10$) is left as an exercise to the reader...
This first answer will be edited by comparing it to an analytical solution using calculus (much easier, but with a surprise Sage bug...).
 | 2 | No.2 Revision |
Okay. After 12 days, your (hypothetic) homework is past due. Let's look at a couple of solutions.
"when you're lost, draw what you know." Undergrads' wisdom. Let's see:
Without loss of generality, set up a framework placong placing the fence center in $O=(0,0)$ and the tether anchor in $A=(r_0,0)$. In this framework a point $(x,y)$ is edible by the goat if it is :
- inside the fence, implying $x^2+y^2<=r_0^2$, and
- closer to the tether's anchor than $r_1$, implying $(r-x)^2+y^2<=r1^2$.
In other words, the edible region is the intersection of two disks $D_0$, centered in $O$ with radius $r_0$ and $D_1$, centered in $A$ with radius $r_1$. This region can be exactly partitioned by the straight line segment joining the intersections of the two circles boundaries of these disks:

Each of these regions is the intersection of a disk of radius $r$ and a half-plane cutting the disk at a distance $X<=r$ of its center.
Therefore, a first, (almost) purely geometrical, solution to your problem is to derive the area of such a surface, and apply it to both the "yellow" and the "red" surfaces. Let's consider the "yellow" one, delimited bu th arc $B'AB$ and the straight segment $BB'$. This surface is symmetric about $OA$ ; therefore, its area is twice of the surface bounded by the arc $AB$ and the straight segments $BX$ and $XA$.
This latter surface can be in turn considered as the difference between
- the circular sector delimited by$OA$, $OB$, and
- the arc $AB$ and the triangle $BOX$.
Let's call $\theta$ the angle $\widehat{AOB}$. It can be determined from the position of $B$. We have of course $\cos\theta=\frac{OX}{r}=\frac{B_x}{r}$ and $\tan\theta={B_y}{B_x}$. At the high school level, this "determination" is a bit fuzzy, but will be clarified in first year of college...
The circular sector has area $\frac{r^2\theta}{2}$, the triangle has area $\frac{OX*XB}{2}=\frac{B_x B_y}{2}$. The yellow surface has area twice their difference, therefore $r_0^2 \theta - B_x\cdot B_y$.
For similar reasons (left to the reader as an exercise ; beware the signs !), with $\cos\theta_1=\frac{B_y}{r_1}$, the "red" sector has area $r_1^2\theta_1-(r_0-B_x) B_y$.
All that is lacking are the coordinates of $B$ which are determined by the fact that it belongs to both the boundary circles (the fence and the tether). Since there are two solution points, we'll select the one with positive ordinate :
x,y,r_0,r_1=var("x,y,r_0,r_1")
assume(x,"real",y,"real",r_0>0,r_1>0,r_1<2*r_0)
O=vector([0,0])
A=vector([r_0,0])
b=vector([x,y])
E0=(b-O).norm()^2==r_0^2
E1=(b-A).norm()^2==r_1^2
Sol=solve([E0, E1],[x,y], solution_dict=True)
if bool(Sol[0].get(y)>0):
B=vector([Sol[0].get(x),Sol[0].get(y)])
else:
B=vector([Sol[1].get(x),Sol[1].get(y)])
X=B[0]
Y=B[1]
That gives us $B=\left(\frac{2 \, r_{0}^{2} - r_{1}^{2}}{2 \, r_{0}},\ \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}}{2 \, r_{0}}\right)$.
This also determines the angle $\theta=\widehat{AOB}$ by either theta=arccos(X/r_0) or theta=arctan2(Y,X) (Note : the third "obvious" choice, theta=arcsin(Y./r_0 is unsuitable here, given the choice of branches of Sage's implementation of arcsin). We determine $\theta_1$ in a similar way (again, mind the signs...).
Summing the partial areas and finding the root (value of $r_1$ leaving an edible area of 10 when $r_0=10$) is left as an exercise to the reader...
This first answer will be edited by comparing it to an analytical solution using calculus (much easier, but with a surprise Sage bug...).
 | 3 | No.3 Revision |
Okay. After 12 days, your (hypothetic) homework is past due. Let's look at a couple of solutions.
"when you're lost, draw what you know." Undergrads' wisdom. Let's see:
Without loss of generality, set up a framework placing the fence center in $O=(0,0)$ and the tether anchor in $A=(r_0,0)$. In this framework a point $(x,y)$ is edible by the goat if it is :
- inside the fence, implying $x^2+y^2<=r_0^2$, and
- closer to the tether's anchor than $r_1$, implying $(r-x)^2+y^2<=r1^2$.
In other words, the edible region is the intersection of two disks $D_0$, centered in $O$ with radius $r_0$ and $D_1$, centered in $A$ with radius $r_1$. This region can be exactly partitioned by the straight line segment joining the intersections of the two circles boundaries of these disks:

Each of these regions is the intersection of a disk of radius $r$ and a half-plane cutting the disk at a distance $X<=r$ of its center.
Therefore, a first, (almost) purely geometrical, solution to your problem is to derive the area of such a surface, and apply it to both the "yellow" and the "red" surfaces. Let's consider the "yellow" one, delimited bu th arc $B'AB$ and the straight segment $BB'$. This surface is symmetric about $OA$ ; therefore, its area is twice of the surface bounded by the arc $AB$ and the straight segments $BX$ and $XA$.
This latter surface can be in turn considered as the difference between
- the circular sector delimited by$OA$, $OB$, and
- the arc $AB$ and the triangle $BOX$.
Let's call $\theta$ the angle $\widehat{AOB}$. It can be determined from the position of $B$. We have of course $\cos\theta=\frac{OX}{r}=\frac{B_x}{r}$ and $\tan\theta={B_y}{B_x}$. At the high school level, this "determination" is a bit fuzzy, but will be clarified in first year of college...
The circular sector has area $\frac{r^2\theta}{2}$, the triangle has area $\frac{OX*XB}{2}=\frac{B_x B_y}{2}$. The yellow surface has area twice their difference, therefore $r_0^2 \theta - B_x\cdot B_y$.
For similar reasons (left to the reader as an exercise ; beware the signs !), with $\cos\theta_1=\frac{B_y}{r_1}$, the "red" sector has area $r_1^2\theta_1-(r_0-B_x) B_y$.
All that is lacking are the coordinates of $B$ which are determined by the fact that it belongs to both the boundary circles (the fence and the tether). Since there are two solution points, we'll select the one with positive ordinate :
x,y,r_0,r_1=var("x,y,r_0,r_1")
assume(x,"real",y,"real",r_0>0,r_1>0,r_1<2*r_0)
O=vector([0,0])
A=vector([r_0,0])
b=vector([x,y])
E0=(b-O).norm()^2==r_0^2
E1=(b-A).norm()^2==r_1^2
Sol=solve([E0, E1],[x,y], solution_dict=True)
if bool(Sol[0].get(y)>0):
B=vector([Sol[0].get(x),Sol[0].get(y)])
else:
B=vector([Sol[1].get(x),Sol[1].get(y)])
X=B[0]
Y=B[1]
That gives us $B=\left(\frac{2 \, r_{0}^{2} - r_{1}^{2}}{2 \, r_{0}},\ \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}}{2 \, r_{0}}\right)$.
This also determines the angle $\theta=\widehat{AOB}$ by either theta=arccos(X/r_0) or theta=arctan2(Y,X) (Note : the third "obvious" choice, theta=arcsin(Y./r_0 is unsuitable here, given the choice of branches of Sage's implementation of arcsin). We determine $\theta_1$ in a similar way (again, mind the signs...).
Summing the partial areas and finding the root (value of $r_1$ leaving an edible area of 10 when $r_0=10$) is left as an exercise to the reader...
This first answer will be edited by comparing it to an analytical solution using calculus (much easier, but with a surprise Sage bug...).
EDIT : Now, an analytical solution using all-singin', all-dancin' calculus.
Let's consider an element of the "yellow" surface : an (infinitely) small vertical strip delimited bu the lines of equation $x=t$ and $x=t+dt$. The surface of this strip will be $(y_u(t)-y_l(t))dt$, where $(t, y_l(t)$ and $(t, y_u(t)$ satisfy $E0$. The total "yellow" area will be the summation of such elemental areas from $t=X$ to $t=r_0$, i.e. $\displaystyle{\int_X^{r_0} (y_u(t)-y_l(t)) dt}$.
Our previous work already gave us $X$. We need to compute explicitly the bounds $y_l$ and $y_u$, and the integral:
Sol0=solve(E0,y)
Y0l(x)=Sol0[0].rhs()
Y0u(x)=Sol0[1].rhs()
g0(x)=(Y0u-Y0l)(x).integrate(x)
Yellow=(g0(r_0)-g0(X)).expand().factor()
A couple notes:
We should be able to obtain directly the definite integral
integrate((Y0u-Y0l)(t), t, X, r_0); but we aren't : Trac#27816 will crash Sage...The integral, $\frac{2 \, \pi r_{0}^{3} + 4 \, r_{0}^{3} \arcsin\left(-\frac{2 \, r_{0}^{2} - r_{1}^{2}}{2 \, r_{0}^{2}}\right) - 2 \, \sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{0} r_{1} + \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}^{3}}{r_{0}}}{4 \, r_{0}}$, bears some similarity with the geometrical solution seen above. This not random...
For the same reasons, we can get the area of the "red" surface :
Sol1=solve(E1,y)
Y1l(x)=Sol1[0].rhs()
Y1u(x)=Sol1[1].rhs()
g1(x)=(Y1u-Y1l)(x).integrate(x)
Red=(g1(X)-g1(r_0-r_1)).expand().factor()
which allows us to compute the expression of the edible fraction as a finction of the fence radius and the tether length :
EdibleFraction(r_0,r_1)=((Yellow+Red)/(pi*r_0^2)).expand().factor()
That is
$$ \frac{\frac{{\left(2 \, \pi r_{0} - 4 \, r_{0} arcsin\left(\frac{r_{1}}{2 \, r_{0}}\right) - \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}}{r_{0}}\right)} r_{1}^{2}}{r_{0}} + \frac{2 \, \pi r_{0}^{3} + 4 \, r_{0}^{3} arcsin\left(-\frac{2 \, r_{0}^{2} - r_{1}^{2}}{2 \, r_{0}^{2}}\right) - 2 \, \sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{0} r_{1} + \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}^{3}}{r_{0}}}{r_{0}}}{400 \, \pi} $$
which looks reasonable:
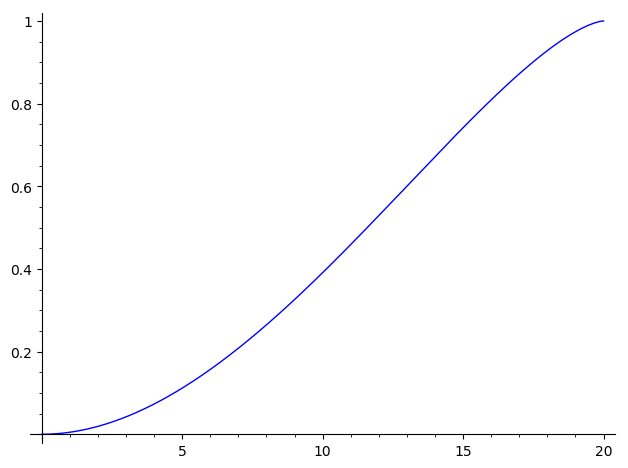
The numerical answer is immediate :
sage: find_root(lambda u:EdibleFraction(10,u)-1/2, 0, 20)
11.587284730181219
One can check that trying to get the definite integral directly gives curipis results :
sympycan't give us an usable answer ;fricasgives a different answer, usingarctaninstead ofarcsin(we saw that this was another possibility) ;giaccan do the integration, but this result can't be used numerically ; this is discussed onsage-devel, but not yet filed as a bug.mathematicaneeds a bit of rewriting (it doesn't tolerate underscore in variable names...), and gives a solution close to the one given byfricas.
Next installment : numerical integration :
Why you shouldn't.
Why you sometimes have to.
How not to do it.
How to speed it
Use of Cython.
Trading speed for precision with stochastic integration.
Stay tuned...
 | 4 | No.4 Revision |
Okay. After 12 days, your (hypothetic) homework is past due. Let's look at a couple of solutions.
"when you're lost, draw what you know." Undergrads' wisdom. Let's see:
Without loss of generality, set up a framework placing the fence center in $O=(0,0)$ and the tether anchor in $A=(r_0,0)$. In this framework a point $(x,y)$ is edible by the goat if it is :
- inside the fence, implying $x^2+y^2<=r_0^2$, and
- closer to the tether's anchor than $r_1$, implying $(r-x)^2+y^2<=r1^2$.
In other words, the edible region is the intersection of two disks $D_0$, centered in $O$ with radius $r_0$ and $D_1$, centered in $A$ with radius $r_1$. This region can be exactly partitioned by the straight line segment joining the intersections of the two circles boundaries of these disks:

Each of these regions is the intersection of a disk of radius $r$ and a half-plane cutting the disk at a distance $X<=r$ of its center.
Therefore, a first, (almost) purely geometrical, solution to your problem is to derive the area of such a surface, and apply it to both the "yellow" and the "red" surfaces. Let's consider the "yellow" one, delimited bu th arc $B'AB$ and the straight segment $BB'$. This surface is symmetric about $OA$ ; therefore, its area is twice of the surface bounded by the arc $AB$ and the straight segments $BX$ and $XA$.
This latter surface can be in turn considered as the difference between
- the circular sector delimited by$OA$, $OB$, and
- the arc $AB$ and the triangle $BOX$.
Let's call $\theta$ the angle $\widehat{AOB}$. It can be determined from the position of $B$. We have of course $\cos\theta=\frac{OX}{r}=\frac{B_x}{r}$ and $\tan\theta={B_y}{B_x}$. At the high school level, this "determination" is a bit fuzzy, but will be clarified in first year of college...
The circular sector has area $\frac{r^2\theta}{2}$, the triangle has area $\frac{OX*XB}{2}=\frac{B_x B_y}{2}$. The yellow surface has area twice their difference, therefore $r_0^2 \theta - B_x\cdot B_y$.
For similar reasons (left to the reader as an exercise ; beware the signs !), with $\cos\theta_1=\frac{B_y}{r_1}$, the "red" sector has area $r_1^2\theta_1-(r_0-B_x) B_y$.
All that is lacking are the coordinates of $B$ which are determined by the fact that it belongs to both the boundary circles (the fence and the tether). Since there are two solution points, we'll select the one with positive ordinate :
x,y,r_0,r_1=var("x,y,r_0,r_1")
assume(x,"real",y,"real",r_0>0,r_1>0,r_1<2*r_0)
O=vector([0,0])
A=vector([r_0,0])
b=vector([x,y])
E0=(b-O).norm()^2==r_0^2
E1=(b-A).norm()^2==r_1^2
Sol=solve([E0, E1],[x,y], solution_dict=True)
if bool(Sol[0].get(y)>0):
B=vector([Sol[0].get(x),Sol[0].get(y)])
else:
B=vector([Sol[1].get(x),Sol[1].get(y)])
X=B[0]
Y=B[1]
That gives us $B=\left(\frac{2 \, r_{0}^{2} - r_{1}^{2}}{2 \, r_{0}},\ \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}}{2 \, r_{0}}\right)$.
This also determines the angle $\theta=\widehat{AOB}$ by either theta=arccos(X/r_0) or theta=arctan2(Y,X) (Note : the third "obvious" choice, theta=arcsin(Y./r_0 is unsuitable here, given the choice of branches of Sage's implementation of arcsin). We determine $\theta_1$ in a similar way (again, mind the signs...).
Summing the partial areas and finding the root (value of $r_1$ leaving an edible area of 10 when $r_0=10$) is left as an exercise to the reader...
This first answer will be edited by comparing it to an analytical solution using calculus (much easier, but with a surprise Sage bug...).
EDIT : Now, an analytical solution using all-singin', all-dancin' calculus.
Let's consider an element of the "yellow" surface : an (infinitely) small vertical strip delimited bu the lines of equation $x=t$ and $x=t+dt$. The surface of this strip will be $(y_u(t)-y_l(t))dt$, where $(t, y_l(t)$ and $(t, y_u(t)$ satisfy $E0$. The total "yellow" area will be the summation of such elemental areas from $t=X$ to $t=r_0$, i.e. $\displaystyle{\int_X^{r_0} (y_u(t)-y_l(t)) dt}$.
Our previous work already gave us $X$. We need to compute explicitly the bounds $y_l$ and $y_u$, and the integral:
Sol0=solve(E0,y)
Y0l(x)=Sol0[0].rhs()
Y0u(x)=Sol0[1].rhs()
g0(x)=(Y0u-Y0l)(x).integrate(x)
Yellow=(g0(r_0)-g0(X)).expand().factor()
A couple notes:
We should be able to obtain directly the definite integral
integrate((Y0u-Y0l)(t), t, X, r_0); but we aren't : Trac#27816 will crash Sage...The integral, $\frac{2 \, \pi r_{0}^{3} + 4 \, r_{0}^{3} \arcsin\left(-\frac{2 \, r_{0}^{2} - r_{1}^{2}}{2 \, r_{0}^{2}}\right) - 2 \, \sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{0} r_{1} + \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}^{3}}{r_{0}}}{4 \, r_{0}}$, bears some similarity with the geometrical solution seen above. This not random...
For the same reasons, we can get the area of the "red" surface :
Sol1=solve(E1,y)
Y1l(x)=Sol1[0].rhs()
Y1u(x)=Sol1[1].rhs()
g1(x)=(Y1u-Y1l)(x).integrate(x)
Red=(g1(X)-g1(r_0-r_1)).expand().factor()
which allows us to compute the expression of the edible fraction as a finction of the fence radius and the tether length :
EdibleFraction(r_0,r_1)=((Yellow+Red)/(pi*r_0^2)).expand().factor()
That is
$$ \frac{\frac{{\left(2 \, \pi r_{0} - 4 \, r_{0} arcsin\left(\frac{r_{1}}{2 \, r_{0}}\right) - \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}}{r_{0}}\right)} r_{1}^{2}}{r_{0}} + \frac{2 \, \pi r_{0}^{3} + 4 \, r_{0}^{3} arcsin\left(-\frac{2 \, r_{0}^{2} - r_{1}^{2}}{2 \, r_{0}^{2}}\right) - 2 \, \sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{0} r_{1} + \frac{\sqrt{4 \, r_{0}^{2} - r_{1}^{2}} r_{1}^{3}}{r_{0}}}{r_{0}}}{400 \, \pi} $$
which looks reasonable:

The numerical answer is immediate :
sage: find_root(lambda u:EdibleFraction(10,u)-1/2, 0, 20)
11.587284730181219
One can check that trying to get the definite integral directly gives curipis curious results :
sympycan't give us an usable answer ;fricasgives a different answer, usingarctaninstead ofarcsin(we saw that this was another possibility) ;giaccan do the integration, but this result can't be used numerically ; this is discussed onsage-devel, but not yet filed as a bug.mathematicaneeds a bit of rewriting (it doesn't tolerate underscore in variable names...), and gives a solution close to the one given byfricas.
Next installment : numerical integration :
Why you shouldn't.
Why you sometimes have to.
How not to do it.
How to speed it
Use of Cython.
Trading speed for precision with stochastic integration.
Stay tuned...
