Revision history [back]
 | 1 | initial version |
For convenience we can define
algebraic_connectivity = lambda g: sorted(list(set(g.laplacian_matrix().eigenvalues())))[1]Then we can obtain at once
G = max((g for g in graphs(7) if g.girth() == 4), key=algebraic_connectivity)But this assumes there is only one maximum. Actually we should be more careful:
my_graphs = [g for g in graphs(7) if g.girth() == 4]
from collections import defaultdict
acs = defaultdict(list)
for g in my_graphs:
ac = algebraic_connectivity(g)
acs[ac].append(g)
max_ac = max(acs.keys())
print 'There are {} graphs of (maximal) algebraic connectivity {}'.format(len(acs[max_ac]), max_ac)
for g in acs[max_ac]:
show(g)Output:
There are 2 graphs of (maximal) algebraic connectivity 3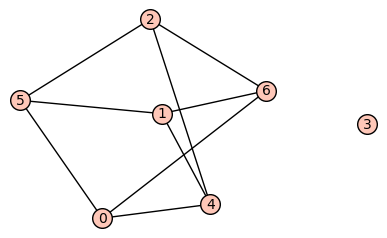
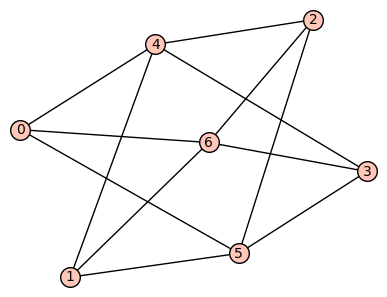
 | 2 | No.2 Revision |
For convenience we can define
algebraic_connectivity = lambda g: sorted(list(set(g.laplacian_matrix().eigenvalues())))[1]
sorted(g.laplacian_matrix().eigenvalues())[1]Then we can obtain at once
G = max((g for g in graphs(7) if g.girth() == 4), key=algebraic_connectivity)But this assumes there is only one maximum. Actually If we should want to be more careful:on the safe side:
my_graphs = [g for g in graphs(7) if g.girth() == 4]
from collections import defaultdict
acs = defaultdict(list)
for g in my_graphs:
ac = algebraic_connectivity(g)
acs[ac].append(g)
max_ac = max(acs.keys())
print 'There are {} graphs of (maximal) algebraic connectivity {}'.format(len(acs[max_ac]), max_ac)
for g in acs[max_ac]:
show(g)Output:
There are 2 1 graphs of (maximal) algebraic connectivity 3

 | 3 | No.3 Revision |
For convenience we can define
algebraic_connectivity = lambda g: sorted(g.laplacian_matrix().eigenvalues())[1]Then we can obtain at once
G = max((g for g in graphs(7) if g.girth() == 4), key=algebraic_connectivity)But this assumes there is only one maximum. If we want to be more on the safe side:
my_graphs = [g for g in graphs(7) if g.girth() == 4]
from collections import defaultdict
acs = defaultdict(list)
for g in my_graphs:
ac = algebraic_connectivity(g)
QQbar(algebraic_connectivity(g)) # ensure keys are always in QQbar, even if rational
acs[ac].append(g)
max_ac = max(acs.keys())
print 'There print('There are {} graphs of (maximal) algebraic connectivity {}'.format(len(acs[max_ac]), max_ac)
max_ac))
for g in acs[max_ac]:
show(g)Output:
There are 1 graphs of (maximal) algebraic connectivity 3

