Ask Your Question

Revision history [back]

Here is a quick and dirty no-brain method:

First, we can iterate over all connected graphs of a given size up to isomorphism, see:

sage: graphs.nauty_geng?

Regarding the spectral radius, note that the spectral radius method is numerical, so there will be some noise preventing us to detect graphs with the same eigenvalue. So, we will use the largest eigenvalue of the adjacency matrix, wich is an exact algebraic number:

sage: G = graphs.RandomGNP(10,1/2)
sage: G.spectral_radius()
(4.885867917434971, 4.885867917912396)
sage: max(G.adjacency_matrix().eigenvalues())
4.885867917602611?

So, let us pick a not-so-small class of connected graphs, say graphs with 8 vertices. And let us classify each of them according to their spectral radius : we make a (lazy) dictionary that maps each spectral radius to the list of graphs with that spectral radius:

sage: from collections import defaultdict
sage: d = defaultdict(list
sage: for G in graphs.nauty_geng('8c'):
....:     d[max(G.adjacency_matrix().eigenvalues())] += [G]

We can see that there are 10350 possible eigenvalues: 

sage: len(d)
10350

So let us restrict to the eigenvalues with more than one corresponding graph:

sage: dd = {i:d[i] for i in d if len(d[i])>1}
sage: len(dd)
1147

Nicer. Just to get an insight, let us look at the maximal classes:

sage: max(len(dd[i]) for i in dd)
23
sage: ddd = {i:d[i] for i in d if len(d[i])==23}
sage: len(ddd)
1

So, there is exactly one eigenvalue for which there are 23 graphs with that spectral radius. Let us inspect it further:

The eigenvalue is:

sage: e = next(iter(ddd)) ; e
3.236067977499790?
sage: e.radical_expression()
sqrt(5) + 1

The corresponding list of graphs is:

sage: L = ddd[e]

Now we can see if there are good candidates:

sage: for G in L:
....:     print(G.diameter(), G.num_edges()) 
(+Infinity, 8)
(+Infinity, 10)
(+Infinity, 9)
(+Infinity, 9)
(3, 11)
(4, 11)
(+Infinity, 9)
(+Infinity, 9)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(3, 11)
(3, 12)
(5, 11)
(3, 12)
(3, 12)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(4, 12)

We can see that with the same spectral radius e there are graphs on 8 vertices with diameter and number of edges (3,11) and (4,12) respectively:

sage: G1,G2 = L[4], L[-1]
sage: G1.diameter()
3
sage: G2.diameter()
4
sage: G1.num_edges()
11
sage: G2.num_edges()
12
sage: G1.spectral_radius()
(3.2360679773376506, 3.2360679776151673)
sage: G2.spectral_radius()
(3.236067977288281, 3.2360679776071106)

We are lucky ! If no such example were found, we would have to inspect all elements of dd.

Here is a quick and dirty no-brain method:

First, we can iterate over all connected graphs of a given size up to isomorphism, see:

sage: graphs.nauty_geng?

Regarding the spectral radius, note that the spectral radius method is numerical, so there will be some noise preventing us to detect graphs with the same eigenvalue. So, we will use the largest eigenvalue of the adjacency matrix, wich is an exact algebraic number:

sage: G = graphs.RandomGNP(10,1/2)
sage: G.spectral_radius()
(4.885867917434971, 4.885867917912396)
sage: max(G.adjacency_matrix().eigenvalues())
4.885867917602611?

So, let us pick a not-so-small class of connected graphs, say graphs with 8 vertices. And let us classify each of them according to their spectral radius : we make a (lazy) dictionary that maps each spectral radius to the list of graphs with that spectral radius:

sage: from collections import defaultdict
sage: d = defaultdict(list
sage: for G in graphs.nauty_geng('8c'):
....:     d[max(G.adjacency_matrix().eigenvalues())] += [G]

We can see that there are 10350 possible eigenvalues: 

sage: len(d)
10350

So let us restrict to the eigenvalues with more than one corresponding graph:

sage: dd = {i:d[i] for i in d if len(d[i])>1}
sage: len(dd)
1147

Nicer. Just to get an insight, let us look at the maximal classes:

sage: max(len(dd[i]) for i in dd)
23
sage: ddd = {i:d[i] for i in d if len(d[i])==23}
sage: len(ddd)
1

So, there is exactly one eigenvalue for which there are 23 graphs with that spectral radius. Let us inspect it further:

The eigenvalue is:

sage: e = next(iter(ddd)) ; e
3.236067977499790?
sage: e.radical_expression()
sqrt(5) + 1

The corresponding list of graphs is:

sage: L = ddd[e]

Now we can see if there are good candidates:

sage: for G in L:
....:     print(G.diameter(), G.num_edges()) 
(+Infinity, 8)
(+Infinity, 10)
(+Infinity, 9)
(+Infinity, 9)
(3, 11)
(4, 11)
(+Infinity, 9)
(+Infinity, 9)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(3, 11)
(3, 12)
(5, 11)
(3, 12)
(3, 12)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(4, 12)

We can see that with the same spectral radius e there are graphs on 8 vertices with diameter and number of edges (3,11) and (4,12) respectively:

sage: G1,G2 = L[4], L[-1]
sage: G1.diameter()
3
sage: G2.diameter()
4
sage: G1.num_edges()
11
sage: G2.num_edges()
12
sage: G1.spectral_radius()
(3.2360679773376506, 3.2360679776151673)
sage: G2.spectral_radius()
(3.236067977288281, 3.2360679776071106)

Here are the pictures of the candidates:

G1

G2

We are lucky ! If no such example were found, we would have to inspect all elements of dd.

Here is a quick and dirty no-brain method:

First, we can iterate over all connected graphs of a given size up to isomorphism, see:

sage: graphs.nauty_geng?

Regarding the spectral radius, note that the spectral radius method is numerical, so there will be some noise preventing us to detect graphs with the same eigenvalue. So, we will use the largest eigenvalue of the adjacency matrix, wich is an exact algebraic number:

sage: G = graphs.RandomGNP(10,1/2)
sage: G.spectral_radius()
(4.885867917434971, 4.885867917912396)
sage: max(G.adjacency_matrix().eigenvalues())
4.885867917602611?

So, let us pick a not-so-small class of connected graphs, say graphs with 8 vertices. And let us classify each of them according to their spectral radius : we make a (lazy) dictionary that maps each spectral radius to the list of graphs with that spectral radius:

sage: from collections import defaultdict
sage: d = defaultdict(list
sage: for G in graphs.nauty_geng('8c'):
....:     d[max(G.adjacency_matrix().eigenvalues())] += [G]

We can see that there are 10350 possible eigenvalues: 

sage: len(d)
10350

So let us restrict to the eigenvalues with more than one corresponding graph:

sage: dd = {i:d[i] for i in d if len(d[i])>1}
sage: len(dd)
1147

Nicer. Just to get an insight, let us look at the maximal classes:

sage: max(len(dd[i]) for i in dd)
23
sage: ddd = {i:d[i] for i in d if len(d[i])==23}
sage: len(ddd)
1

So, there is exactly one eigenvalue for which there are 23 graphs with that spectral radius. Let us inspect it further:

The eigenvalue is:

sage: e = next(iter(ddd)) ; e
3.236067977499790?
sage: e.radical_expression()
sqrt(5) + 1

The corresponding list of graphs is:

sage: L = ddd[e]

Now we can see if there are good candidates:

sage: for G in L:
....:     print(G.diameter(), G.num_edges()) 
(+Infinity, 8)
(+Infinity, 10)
(+Infinity, 9)
(+Infinity, 9)
(3, 11)
(4, 11)
(+Infinity, 9)
(+Infinity, 9)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(3, 11)
(3, 12)
(5, 11)
(3, 12)
(3, 12)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(4, 12)

We can see that with the same spectral radius e there are graphs on 8 vertices with diameter and number of edges (3,11) and (4,12) respectively:

sage: G1,G2 = L[4], L[-1]
sage: G1.diameter()
3
sage: G2.diameter()
4
sage: G1.num_edges()
11
sage: G2.num_edges()
12
sage: G1.spectral_radius()
(3.2360679773376506, 3.2360679776151673)
sage: G2.spectral_radius()
(3.236067977288281, 3.2360679776071106)

Here are the pictures of the candidates:

G1

G2

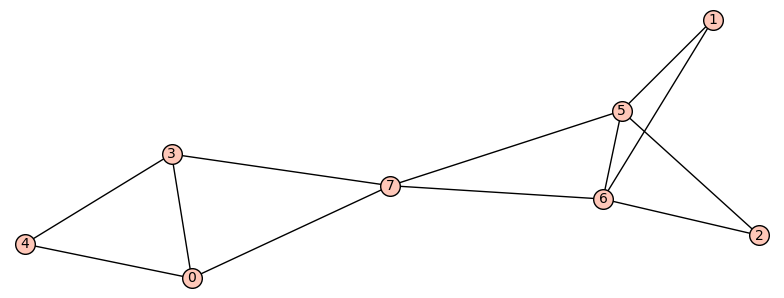
We are lucky ! If no such example were found, we would have to inspect all elements of dd.

EDIT Actualy i did a typo in the use of graphs.nauty_geng('8c'), which explains why we got disconnected graphs (infinite diameter). The correct syntax is graphs.nauty_geng('8 -c'). Instead we get 9820 different spectral radius, 926 spectral radius with at least two graphs, the spectral radius with the largest number of graphs is 1/2*sqrt(17) + 3/2, and there are 12 such graphs. In that list, the pairs (diameter, num_edges) is (3,12), (4,12), (3,13), (4,13), (2,14), (3,14).

Here is a quick and dirty no-brain method:

First, we can iterate over all connected graphs of a given size up to isomorphism, see:

sage: graphs.nauty_geng?

Regarding the spectral radius, note that the spectral radius method is numerical, so there will be some noise preventing us to detect graphs with the same eigenvalue. So, we will use the largest eigenvalue of the adjacency matrix, wich is an exact algebraic number:

sage: G = graphs.RandomGNP(10,1/2)
sage: G.spectral_radius()
(4.885867917434971, 4.885867917912396)
sage: max(G.adjacency_matrix().eigenvalues())
4.885867917602611?

So, let us pick a not-so-small class of connected graphs, say graphs with 8 vertices. And let us classify each of them according to their spectral radius : we make a (lazy) dictionary that maps each spectral radius to the list of graphs with that spectral radius:

sage: from collections import defaultdict
sage: d = defaultdict(list
sage: for G in graphs.nauty_geng('8c'):
....:     d[max(G.adjacency_matrix().eigenvalues())] += [G]

We can see that there are 10350 possible eigenvalues: 

sage: len(d)
10350

So let us restrict to the eigenvalues with more than one corresponding graph:

sage: dd = {i:d[i] for i in d if len(d[i])>1}
sage: len(dd)
1147

Nicer. Just to get an insight, let us look at the maximal classes:

sage: max(len(dd[i]) for i in dd)
23
sage: ddd = {i:d[i] for i in d if len(d[i])==23}
sage: len(ddd)
1

So, there is exactly one eigenvalue for which there are 23 graphs with that spectral radius. Let us inspect it further:

The eigenvalue is:

sage: e = next(iter(ddd)) ; e
3.236067977499790?
sage: e.radical_expression()
sqrt(5) + 1

The corresponding list of graphs is:

sage: L = ddd[e]

Now we can see if there are good candidates:

sage: for G in L:
....:     print(G.diameter(), G.num_edges()) 
(+Infinity, 8)
(+Infinity, 10)
(+Infinity, 9)
(+Infinity, 9)
(3, 11)
(4, 11)
(+Infinity, 9)
(+Infinity, 9)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(3, 11)
(3, 12)
(5, 11)
(3, 12)
(3, 12)
(+Infinity, 10)
(3, 12)
(+Infinity, 11)
(4, 12)

We can see that with the same spectral radius e there are graphs on 8 vertices with diameter and number of edges (3,11) and (4,12) respectively:

sage: G1,G2 = L[4], L[-1]
sage: G1.diameter()
3
sage: G2.diameter()
4
sage: G1.num_edges()
11
sage: G2.num_edges()
12
sage: G1.spectral_radius()
(3.2360679773376506, 3.2360679776151673)
sage: G2.spectral_radius()
(3.236067977288281, 3.2360679776071106)

Here are the pictures of the candidates:

G1

G2

We are lucky ! If no such example were found, we would have to inspect all elements of dd.

EDIT Actualy i did a typo in the use of graphs.nauty_geng('8c'), which explains why we got disconnected graphs (infinite diameter). The correct syntax is graphs.nauty_geng('8 -c'). Instead we get 9820 different spectral radius, 926 spectral radius with at least two graphs, the spectral radius with the largest number of graphs is 1/2*sqrt(17) + 3/2, and there are 12 such graphs. In that list, the pairs (diameter, num_edges) is (3,12), (4,12), (3,13), (4,13), (2,14), (3,14).

EDIT As requested in the commenrs, here is an automatic way do the whole search using a function:

def search(n=3):
    r"""
    Search, among connected graphs of size n, two graphs with the same spectral
    radius but different diameter and number of edges.
    """
    from collections import defaultdict
    d = defaultdict(list)
    for G in graphs.nauty_geng('{} -c'.format(n)):
        d[max(G.adjacency_matrix().eigenvalues())] += [G]
    for s in d:
        if len(d[s]) > 1:
            for g1 in d[s]:
                for g2 in d[s]:
                    if g1.diameter() != g2.diameter() and g1.num_edges() != g2.num_edges():
                        return (g1, g2)
    return

You can see that there are no candidates of size 5:

sage: f = search(5)
sage: f

But there are candidates of size 6:

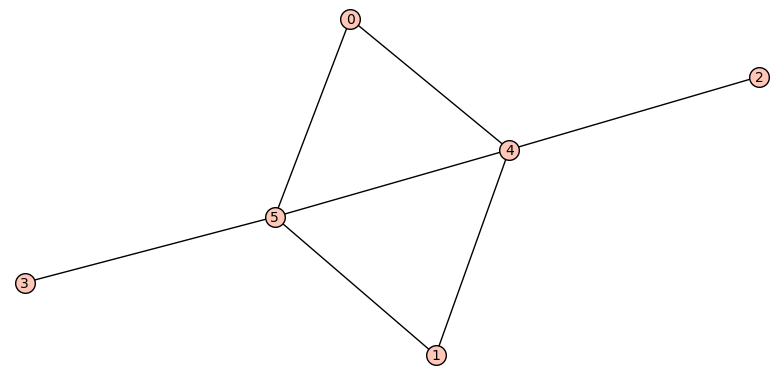
sage: f = search(6)
sage: f
(Graph on 6 vertices, Graph on 6 vertices)
sage: g0, g1 = f
sage: g0.diameter()
3
sage: g1.diameter()
2
sage: g0.num_edges()
7
sage: g1.num_edges()
8
sage: g0.spectral_radius()
(2.7912878473346825, 2.791287847569842)
sage: g1.spectral_radius()
(2.791287847405329, 2.7912878475910357)
sage: g0.plot()
Launched png viewer for Graphics object consisting of 14 graphics primitives
sage: g1.plot()
Launched png viewer for Graphics object consisting of 15 graphics primitives

g0

g1
Copyright Sage, 2010. Some rights reserved under creative commons license. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.
about | faq | help | privacy policy | terms of service
Powered by Askbot version 0.7.59