Revision history [back]
 | 1 | initial version |
You got:
sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line (in the interval [π,π]): - if θ is an integer multiple of π\2, then ϕ=0,±π is the solution set. - in general, there are exactly 2 intersections. - if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.
 | 2 | No.2 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line (in the interval [π,π]):
- if θ is an integer multiple of π\2, π/2, then ϕ=0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions. assumptions.
 | 3 | No.3 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line (in line, and by periodicity we can reason in the interval $[\pi, \pi]$):
- \pi]$:
- if θ is an integer multiple of π/2, then ϕ=0,±π is the solution
set. -set. - in general, there are exactly 2
intersections. -intersections. - if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.
 | 4 | No.4 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[\pi, $[-\pi, \pi]$:
- if θ is an integer multiple of π/2, then ϕ=0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.
 | 5 | No.5 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π]:
- if θ is an integer multiple of
π/2,π, then ϕ=0,±π is the solution set. - in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.
 | 6 | No.6 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π]:
- if θ is an integer multiple of π, then
$\phi = {0,\pm${0,\pm \pi}$ is the solution set. - in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.
 | 7 | No.7 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$:\pi]$, recall that:
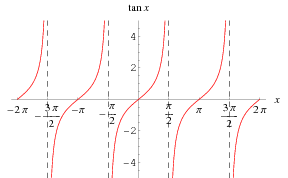
- if θ is an integer multiple of π, then 0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.
 | 8 | No.8 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π], recall that:

- if θ is an integer multiple of π, then 0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.
 | 9 | No.9 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π], recall that:

- if θ is an integer multiple of π, then 0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then we have no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy SymPy solve or solveset.. the new solveset.. but maybe I'm missing to pass some extra assumptions.information.
 | 10 | No.10 Revision |
You got:
sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π], recall that:

- if θ is an integer multiple of π, then 0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then
we havethere exists a value of θ for which the denominator vanishes, and there is no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.
 | 11 | No.11 Revision |
You It seems to me that the hard work is already done properly by the solver. Finally, you got:
sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π], recall that:

- if θ is an integer multiple of π, then 0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then there exists a value of θ for which the denominator vanishes, and there is no solution.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.
 | 12 | No.12 Revision |
It seems to me that the hard work is already done properly by the solver. Finally, you got:
sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π], recall that:

- if θ is an integer multiple of π, then 0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then there exists a value of θ for which the denominator
vanishes, and there is no solution.vanishes; the solution set is ±π/2.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.
 | 13 | No.13 Revision |
It seems to me that the hard work is already done properly by the solver. Finally, you got:
sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π], recall that:

- if θ is an integer multiple of π, then 0,±π is the solution set.
- in general, there are exactly 2 intersections.
- if the values of M1 and M2 allow it (|M1/M2|≤1), then there exists a value of θ for which the denominator
vanishes;vanishes, but the solution set is ±π/2.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.
 | 14 | No.14 Revision |
It seems to me that the hard work is already done properly by the solver. Finally, you got:
sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)Which is: ((cos(θ)sin(ϕ)+cos(ϕ)sin(θ))M2−M1sin(ϕ)M2,[sin(ϕ)=−M2cos(ϕ)sin(θ)M2cos(θ)−M1])
Hence, the solution for ϕ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval [−π,π], recall that:

- if θ is an integer multiple of π, then 0,±π is the solution set.
- in general, there are exactly 2
intersections.intersections (and the solutions differ by π). - if the values of M1 and M2 allow it (|M1/M2|≤1), then there exists a value of θ for which the denominator vanishes, but the solution set is ±π/2.
Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.
