Revision history [back]

You got:

sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line (in the interval $[\pi, \pi]$): - if $\theta$ is an integer multiple of $\pi\2$, then $\phi = {0,\pm \pi}$ is the solution set. - in general, there are exactly $2$ intersections. - if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.

You got:

sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line (in the interval $[\pi, \pi]$): - if $\theta$ is an integer multiple of $\pi\2$, $\pi/2$, then $\phi = {0,\pm \pi}$ is the solution set. - in general, there are exactly $2$ intersections. - if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions. assumptions.

You got:

sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line (in line, and by periodicity we can reason in the interval $[\pi, \pi]$): - \pi]$:

• if $\theta$ is an integer multiple of $\pi/2$, then $\phi = {0,\pm \pi}$ is the solution set. - set.
• in general, there are exactly $2$ intersections. - intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.

You got:

sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[\pi, $[-\pi, \pi]$:

• if $\theta$ is an integer multiple of $\pi/2$, then $\phi = {0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.

You got:

sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$:

• if $\theta$ is an integer multiple of $\pi/2$, $\pi$, then $\phi = {0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.

You got:

sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$:

• if $\theta$ is an integer multiple of $\pi$, then $\phi = {0,\pm ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.

You got:

sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$:\pi]$, recall that:

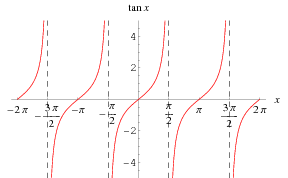
• if $\theta$ is an integer multiple of $\pi$, then ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.

You got:

sage: var("theta phi M_1 M_2")
sage: %display typeset
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$, recall that:

• if $\theta$ is an integer multiple of $\pi$, then ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy solve or solveset.. but maybe I'm missing to pass some extra assumptions.

You got:

sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$, recall that:

• if $\theta$ is an integer multiple of $\pi$, then ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with sympy SymPy solve or solveset.. the new solveset.. but maybe I'm missing to pass some extra assumptions.information.

You got:

sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$, recall that:

• if $\theta$ is an integer multiple of $\pi$, then ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then we have there exists a value of $\theta$ for which the denominator vanishes, and there is no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.

You It seems to me that the hard work is already done properly by the solver. Finally, you got:

sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$, recall that:

• if $\theta$ is an integer multiple of $\pi$, then ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then there exists a value of $\theta$ for which the denominator vanishes, and there is no solution.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.

It seems to me that the hard work is already done properly by the solver. Finally, you got:

sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$, recall that:

• if $\theta$ is an integer multiple of $\pi$, then ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then there exists a value of $\theta$ for which the denominator vanishes, and there is no solution.vanishes; the solution set is $\pm \pi/2$.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.

It seems to me that the hard work is already done properly by the solver. Finally, you got:

sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$, recall that:

• if $\theta$ is an integer multiple of $\pi$, then ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then there exists a value of $\theta$ for which the denominator vanishes; vanishes, but the solution set is $\pm \pi/2$.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.

It seems to me that the hard work is already done properly by the solver. Finally, you got:

sage: var("theta phi M_1 M_2")
sage: f = (sin(theta+phi)-M_1/M_2*sin(phi)).simplify_full()
sage: f, solve(f, phi)

Which is: $$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\frac{{\left(\cos\left(\theta\right) \sin\left(\phi\right) + \cos\left(\phi\right) \sin\left(\theta\right)\right)} M_{2} - M_{1} \sin\left(\phi\right)}{M_{2}}, \left[\sin\left(\phi\right) = -\frac{M_{2} \cos\left(\phi\right) \sin\left(\theta\right)}{M_{2} \cos\left(\theta\right) - M_{1}}\right]\right)$$

Hence, the solution for $\phi$ is obtianed by intersecting the tangent function with a constant line, and by periodicity we can reason in the interval $[-\pi, \pi]$, recall that:

• if $\theta$ is an integer multiple of $\pi$, then ${0,\pm \pi}$ is the solution set.
• in general, there are exactly $2$ intersections.intersections (and the solutions differ by $\pi$).
• if the values of $M_1$ and $M_2$ allow it ($|M_1/M_2| \leq 1$), then there exists a value of $\theta$ for which the denominator vanishes, but the solution set is $\pm \pi/2$.

Remark. I'd be interested to know if there is a way to do this sort of "case study" automatically. I tried with some solver options (explicit, etc.), but it doesn't help. Neither with SymPy solve or the new solveset.. but maybe I'm missing to pass some extra information.