Revision history [back]
 | 1 | initial version |
Would this give you what you are looking for? (assuming your interval is [-1;2]
f(y) = x^4-3*x+8
f.show()
find_local_maximum(f, -1, 2)
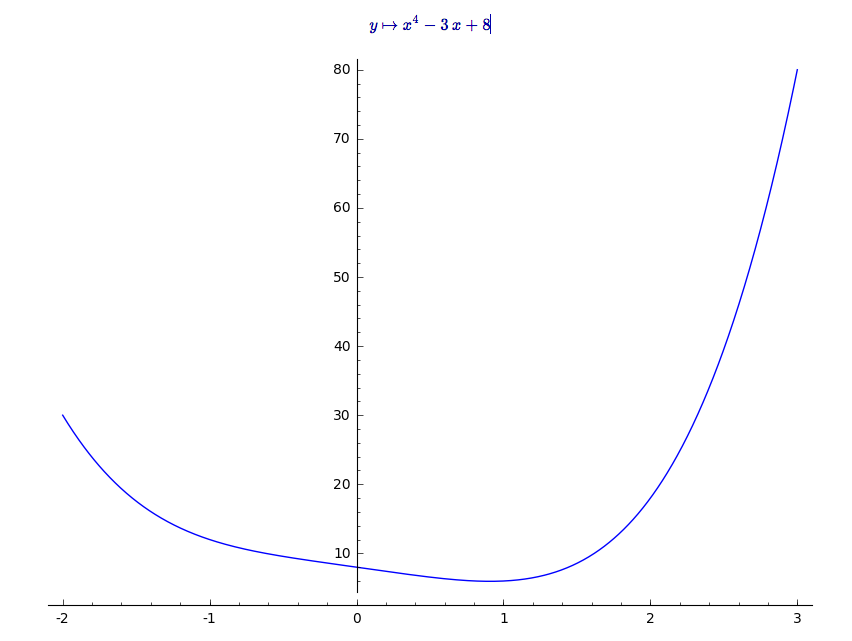
I am generally big on plotting unction like this, you can try to get a feel of your function
plot(f(y), -2,3)
I highly recommend the SageMath Calculus Tutorial if you at all have the time.
 | 2 | No.2 Revision |
Would this give you what you are looking for? (assuming your interval is [-1;2]
f(y) = x^4-3*x+8
f.show()
find_local_maximum(f, -1, 2)
I am generally big on plotting unction like this, you can try to get a feel of your function
plot(f(y), -2,3)

I highly recommend the SageMath Calculus Tutorial if you at all have the time.
Update,
If I run your updated model with your coefficients, e.i.,
f = (1/4)*log(2.02000000000000*x + 1) + (1/2)*log(0.00999999999999979*x + 1) + (1/4)*log(-2*x + 1)
find_local_maximum(diff(f,x), 0, 1)
i get,
(95160969.23167175, 0.50000000262712752)
Could you explain what you expect and why? Did i possibly misinterpret your code? (I did added some parenthesis and some multiplication symbols).
