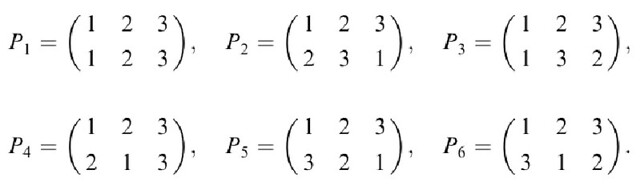bk322's profile - activity
| 2024-04-18 11:37:33 +0200 | received badge | ● Notable Question (source) |
| 2024-04-18 11:37:33 +0200 | received badge | ● Popular Question (source) |
| 2023-08-29 08:28:47 +0200 | received badge | ● Famous Question (source) |
| 2022-01-25 10:40:21 +0200 | received badge | ● Famous Question (source) |
| 2022-01-25 10:40:21 +0200 | received badge | ● Notable Question (source) |
| 2021-09-01 00:17:44 +0200 | received badge | ● Notable Question (source) |
| 2021-09-01 00:17:44 +0200 | received badge | ● Popular Question (source) |
| 2021-03-21 19:34:34 +0200 | received badge | ● Popular Question (source) |
| 2020-04-28 00:14:37 +0200 | received badge | ● Good Answer (source) |
| 2019-12-18 04:53:31 +0200 | received badge | ● Notable Question (source) |
| 2019-03-02 10:04:50 +0200 | received badge | ● Popular Question (source) |
| 2019-03-02 10:04:50 +0200 | received badge | ● Notable Question (source) |
| 2015-01-13 20:48:07 +0200 | received badge | ● Famous Question (source) |
| 2015-01-13 20:46:01 +0200 | received badge | ● Famous Question (source) |
| 2014-12-11 23:51:29 +0200 | received badge | ● Popular Question (source) |
| 2014-06-29 06:56:36 +0200 | received badge | ● Famous Question (source) |
| 2014-06-29 06:56:36 +0200 | received badge | ● Notable Question (source) |
| 2014-06-29 03:15:17 +0200 | marked best answer | Polynomial representation of GF(7)? Why sage would give me polynomial representation of GF(8), but not GF(7)? Maybe there's no such thing as polynomial represenation of GF(7)? |
| 2014-06-29 03:15:17 +0200 | marked best answer | Permutation group: (1234)=(12)(13)(14) How do I show in sage that I tried make use of: but it doesn't do what is needed. |
| 2014-06-29 03:15:17 +0200 | marked best answer | S3's elements Here's elements of Symmetric group of 6th order: S3:
I want to get the same in Sage. So I do: Now I can't find (1,3,2) element in the book. As far as I understand: So my question is to set the correct map from sage to my book... |
| 2014-06-29 03:15:17 +0200 | marked best answer | What can I delete? So I've compiled sage from sources. The sage folder is now 3Gb. I guess I've no need for some files... What can I delete? Is there any reason I should not delete these things? |
| 2014-06-29 03:14:50 +0200 | marked best answer | Symbolic product in Sage? Suppose I'd like to compute How can this be done? I found an old thread, but with no answers. |
| 2013-12-03 16:41:38 +0200 | received badge | ● Taxonomist |
| 2013-10-15 15:07:15 +0200 | received badge | ● Popular Question (source) |
| 2013-10-11 06:33:03 +0200 | received badge | ● Popular Question (source) |
| 2013-06-16 07:38:35 +0200 | marked best answer | Symbolic product in Sage? Take the natural logarithm of your product and you get a sum which can be evaluated: $$\ln\left( \prod_{x=1}^k \frac{1}{x^4} \right) = \sum_{x=1}^k \ln\left(\frac{1}{x^4}\right)$$ ... now take the limit as $k \to \infty$: |
| 2013-06-06 02:39:36 +0200 | received badge | ● Notable Question (source) |
| 2013-02-20 19:53:07 +0200 | received badge | ● Notable Question (source) |
| 2012-11-01 16:46:05 +0200 | received badge | ● Popular Question (source) |
| 2012-10-15 06:58:50 +0200 | received badge | ● Nice Answer (source) |
| 2012-09-23 12:26:34 +0200 | received badge | ● Popular Question (source) |
| 2012-06-19 06:39:28 +0200 | received badge | ● Commentator |
| 2012-06-19 06:39:28 +0200 | commented question | Python thing that doesn't work in Sage, works in pure Python See [here](http://www.sagemath.org/doc/faq/faq-usage.html#i-have-type-issues-using-scipy-cvxopt-or-numpy-from-sage). |
| 2012-06-14 11:23:20 +0200 | commented answer | Symbolic product in Sage? Am... Great, but why post it here? |
| 2012-06-13 10:37:57 +0200 | marked best answer | Check that P3*P6=P4 The problem is that you are comparing lists, not Sage objects. achrzesz gives an answer which compares two Sage group elements, so they are equal. The lists you give are simple Python ordered lists, and as ordered things, certainly aren't the same. Why didn't you just compare By the way, they're not the same. But that's a different issue. They're using the notation of the second row of your notation in your original question, not cycle notation. |
| 2012-06-12 14:45:50 +0200 | commented answer | Check that P3*P6=P4 But mine are also the same. [3, 2, 1] is same as [2, 1, 3], isn't it? |
| 2012-06-12 14:18:09 +0200 | asked a question | Check that P3*P6=P4 Here's elements of Symmetric group of 6th order: S3:
I want to check that P3*P6=P4. it gives: so they are the same actually. But how do I make sage say |
| 2012-06-12 12:52:41 +0200 | marked best answer | S3's elements The results of are given in cycle notation. So the book's equivalent of (1,3,2) is one where 1 becomes 3, 3 becomes 2, and 2 becomes 1, which is P6, if I'm reading correctly. If you want to match the bottom three elements of your matrix, you can simply convert each to a list, or maybe a dict would make the mapping more explicit: |
| 2012-06-12 12:52:40 +0200 | commented answer | S3's elements That's very cool. I did this: `for e in sorted(G): print '{0:>8s}{1:>10s}{2:>19s}'.format(e, e.list(), e.dict())` (I type more then, but it inserts >...) |