Bern's profile - activity

How to get rid of a memory-leak when solving euqations modulo an integer with sage? Hi, I am running into a memory-leak

How to get rid of a memory-leak when solving euqations modulo an integer with sage Hi, I am running into a memory leak

How to get rid of a memory-leak when solving euqations modulo an integer with sage Hi, I am running into a memory leak

Ok, thank you very much. With the grafical user interface with Maple it worked...but not with the terminal version...sorry...Of course, I am still interested, if SAGE also has something similar implemented.

Does Sage have a general implementation of the "affine diagonalization algorithm" for n-dimensional vector spaces?

I found some pseudo-code, see page 15 (in section 3 "affine diagonalization" which begins on page 12) of

• Lecture 21: Surfaces in Robust geometric computation

Searching online led me also to this answer from 2008 where someone does it with Maple:

• Maple primes: Normal forms for quadratic functions

but unfortunately, I cannot open the .mws file (I get an error message concerning the version number).

Thank you very much for the help.

I would like to find with Sage in a quick way all finite lattices having a partial operation $x\cdot y$, defined for $x\geq y$, satisfying the following properties:

(a) $\forall x\geq y\geq z:\ x\cdot z \leq x\cdot y$ and $(x\cdot y)\cdot (x\cdot z) = y\cdot z$

(b) $\forall x\geq y, z:\ x\cdot (y \wedge z) = x\cdot y \wedge x\cdot z$

(c) $(x \vee y)\cdot y = x\cdot (x \wedge y) $

(d) $\forall x\geq y:\ y\leq x\cdot y$ and $(x\cdot y)\cdot y = x$

This is equivalent to having the structure of an MV algebra (see Prop. 44 on page 34 of https://pnp.mathematik.uni-stuttgart.de/iaz/iaz1/Rump/32-35.pdf).

Such lattices are always distributive.

I would be grateful for any help.

Commutativity is not necessary - sorry that I wrote sth. wrong earlier.

Hi,

I would like to ask the following question:

I have recently installed sage 9.1 and wanted to install all the gap packages inside sage.

I tried sage -i gap_packages (and sage -f gap_packages respectively) but I got the following error message which seems to point to a problem with "crypting-0.9".

A quick search showed me that there has already been a problem with this earlier, so I just wanted to ask here, if anybody could help/show me how to resolve this problem.

I work with Kubuntu 20.04, have an VivoBook-ASUSLaptop and downloaded the precompiled sage files.

Thank you very much.

.
.
.
[gap_packages-4.10.2.p1] testdata -> /home/bernhard/Schreibtisch/SageMath/local/var/tmp/sage/build/gap_packages-4.10.2.p1/inst/home/bernhard/Schreibtisch/SageMath/local/share/gap/pkg/cohomolo-1.6.7

[gap_packages-4.10.2.p1] tst -> /home/bernhard/Schreibtisch/SageMath/local/var/tmp/sage/build/gap_packages-4.10.2.p1/inst/home/bernhard/Schreibtisch/SageMath/local/share/gap/pkg/cohomolo-1.6.7

[gap_packages-4.10.2.p1] Building GAP package crypting-0.9

[gap_packages-4.10.2.p1] Using config in /home/bernhard/Schreibtisch/SageMath/local/share/gap/sysinfo.gap
[gap_packages-4.10.2.p1] Building gap_packages-4.10.2.p1
[gap_packages-4.10.2.p1] make[2]: Entering directory '/home/bernhard/Schreibtisch/SageMath/local/var/tmp/sage/build/gap_packages-4.10.2.p1/src/pkg/crypting-0.9'

[gap_packages-4.10.2.p1] /bin/bash /home/bernhard/Schreibtisch/SageMath/local/share/gap/libtool --mode=compile gcc -O2 -g -MQ obj/crypting.lo -MMD -MP -MF obj/.deps/crypting.d -o obj/crypting.lo -I/var/lib/buildbot/slave/binary_pkg/build/source/SageMath/jc4b6yulaujayb9sr94ia88eourzeqip0oidmas391y/local/share/gap/gen -I/var/lib/buildbot/slave/binary_pkg/build/source/SageMath/jc4b6yulaujayb9sr94ia88eourzeqip0oidmas391y/local/share/gap/src -I/var/lib/buildbot/slave/binary_pkg/build/source/SageMath/jc4b6yulaujayb9sr94ia88eourzeqip0oidmas391y/local/share/gap -DHAVE_CONFIG_H -I/var/lib/buildbot/slave/binary_pkg/build/source/SageMath/jc4b6yulaujayb9sr94ia88eourzeqip0oidmas391y/local/include -c src/crypting.c

[gap_packages-4.10.2.p1] libtool: compile:  gcc -O2 -g -MQ obj/crypting.lo -MMD -MP -MF obj/.deps/crypting.d -I/var/lib/buildbot/slave/binary_pkg/build/source/SageMath/jc4b6yulaujayb9sr94ia88eourzeqip0oidmas391y/local/share/gap/gen -I/var/lib/buildbot/slave/binary_pkg/build/source/SageMath/jc4b6yulaujayb9sr94ia88eourzeqip0oidmas391y/local/share/gap/src -I/var/lib/buildbot/slave/binary_pkg/build/source/SageMath/jc4b6yulaujayb9sr94ia88eourzeqip0oidmas391y/local/share/gap -DHAVE_CONFIG_H -I/var/lib/buildbot/slave/binary_pkg/build/source/SageMath/jc4b6yulaujayb9sr94ia88eourzeqip0oidmas391y/local/include -c src/crypting.c  -fPIC -DPIC -o obj/.libs/crypting.o

[gap_packages-4.10.2.p1] src/crypting.c:5:10: fatal error: src/compiled.h: No such file or directory
[gap_packages-4.10.2.p1]     5 | #include "src/compiled.h"          /* GAP headers */
[gap_packages-4.10.2.p1]       |          ^~~~~~~~~~~~~~~~
[gap_packages-4.10.2.p1] compilation terminated.
[gap_packages-4.10.2.p1] make[2]: *** [Makefile:105: obj/crypting.lo] Error 1
[gap_packages-4.10.2.p1] make[2]: Leaving directory '/home/bernhard/Schreibtisch/SageMath/local/var/tmp/sage/build/gap_packages-4.10.2.p1/src/pkg/crypting-0.9'
[gap_packages-4.10.2.p1] ********************************************************************************
[gap_packages-4.10.2.p1] Error building gap_packages-4.10.2.p1
[gap_packages-4.10.2.p1] ********************************************************************************
[gap_packages-4.10.2.p1] 
[gap_packages-4.10.2.p1] real   0m6.918s
[gap_packages-4.10.2.p1] user   0m4.702s
[gap_packages-4.10.2.p1] sys    0m1.209s
[gap_packages-4.10.2.p1] ************************************************************************
[gap_packages-4.10.2.p1] Error installing package gap_packages-4.10.2.p1
[gap_packages-4.10.2.p1] ************************************************************************ 
[gap_packages-4.10.2.p1] Please email sage-devel (http://groups.google.com/group/sage-devel)
[gap_packages-4.10.2.p1] explaining the problem and including the log file
[gap_packages-4.10.2.p1]   /home/bernhard/Schreibtisch/SageMath/logs/pkgs/gap_packages-4.10.2.p1.log  
[gap_packages-4.10.2.p1] Describe your computer, operating system, etc.
[gap_packages-4.10.2.p1] If you want to try to fix the problem yourself, *don't* just cd to
[gap_packages-4.10.2.p1] /home/bernhard/Schreibtisch/SageMath/local/var/tmp/sage/build/gap_packages-4.10.2.p1 and type 'make' or whatever is appropriate.

[gap_packages-4.10.2.p1] Instead, the following commands setup all environment variables
[gap_packages-4.10.2.p1] correctly and load a subshell for you to debug the error:
[gap_packages-4.10.2.p1]   (cd '/home/bernhard/Schreibtisch/SageMath/local/var/tmp/sage/build/gap_packages-4.10.2.p1' && '/home/bernhard/Schreibtisch/SageMath/sage' --buildsh)
[gap_packages-4.10.2.p1] When you are done debugging, you can type "exit" to leave the subshell.
[gap_packages-4.10.2.p1] ************************************************************************
make[1]: *** [Makefile:2143: /home/bernhard/Schreibtisch/SageMath/local/var/lib/sage/installed/gap_packages-4.10.2.p1]
Error 1
make[1]: Leaving directory '/home/bernhard/Schreibtisch/SageMath/build/make'

real    2m13,674s
user    2m6,068s
sys     0m5,643s
***************************************************************
Error building Sage.

The following package(s) may have failed to build (not necessarily
during this run of 'make gap_packages'):

* package:         gap_packages-4.10.2.p1
last build time: Aug 3 22:41
log file:        /home/bernhard/Schreibtisch/SageMath/logs/pkgs/gap_packages-4.10.2.p1.log
build directory: /home/bernhard/Schreibtisch/SageMath/local/var/tmp/sage/build/gap_packages-4.10.2.p1

It is safe to delete any log files and build directories, but they
contain information that is helpful for debugging build problems.
WARNING: If you now run 'make' again, the build directory of the
same version of the package will, by default, be deleted. Set the
environment variable SAGE_KEEP_BUILT_SPKGS=yes to prevent this.

make: *** [Makefile:33: gap_packages] Error 1

Thank you very much for your comment. For example, G=gap.SymmtricGroup(5) and iso= gap.IsomorphismPermGroup(G) I realized that the problem was inside gap and not inside sage...sorry. I can do it with the ctbllib commands StrDescr = gap.NameOfEquivalentLibraryCharacterTable(CTBL) CTBL_Breuer = gap.CharacterTable(StrDescr) Sorry for the confusion and that I was missing a minimal complete example. It would be ok, if you'd like to delete my question.

By the way: The error message is as follows: RuntimeError: Gap produced error output Error, < G > has already a character table

Thank you very much for your comment. I edited the question.

Dear SAGE forum,

I'd like to ask the following question:

Is there an equivalent in SAGE of GAP's "shallowcopy" ?

I'd like to associate to two times the same group two different character tables.

In GAP it is possible to do it as follows:

G:=AlternatingGroup(5);
H:=ShallowCopy(G);
ct_G:=CharacterTable(G);

and to then construct a different character table for H.

When I try to do this in SAGE, I always get the error message that G (!) already has a character table, although I wanted to assign a different (as far as the ordering of the rows and columns are concerned) character table to H (!)

EDIT (20.11.2019):

Here is part of my sage code:

HHHH=gap.Image(iso)
GGGG=gap.ShallowCopy(gap.Image(iso))

# Hier Einschub: CTBL wie in CTBLLib (falls vorhanden) wird nun gemacht:
gap.LoadPackage('"ctbllib"')

def CTBL_Breuer_fert(X):
  StrDescr = gap.StructureDescription(X)
  if gap.IsString(gap.StructureDescription(X)):
    StrDescr = gap.StructureDescription(X)
    CTBL_Breuer = gap.CharacterTable(StrDescr)
    CTBL_Breuer_fertig = gap.CharacterTableWithStoredGroup(X,CTBL_Breuer)
  else:
    CTBL_Breuer_fertig = gap.CharacterTable(X)
  return(CTBL_Breuer_fertig)


CTBL_Breuer_fertig = CTBL_Breuer_fert(HHHH)


# Hier Ende des Einschubs


ccl = [gap.ConjugacyClass(GGGG,x) for x in MAGMA_ccls_GG_for_GAP]

gap.SetConjugacyClasses(GGGG,ccl)
gap.SetUnderlyingGroup(tbl,GGGG)
gap.SetConjugacyClasses(tbl,ccl)
bij=[1..len(ccl)]

MyRecordFile = open("GAP_Record.txt",'w')
print >> MyRecordFile, "bij:=",
print >> MyRecordFile, bij,
print >> MyRecordFile, ";"
print >> MyRecordFile, "myrecfunct:=function()"
print >> MyRecordFile, "local RECOR;"
print >> MyRecordFile, "RECOR:=rec(bijection:=bij);"
print >> MyRecordFile, "return RECOR;"
print >> MyRecordFile, "end;"
MyRecordFile.close()

gap.Read('"GAP_Record.txt"')
recor=gap.myrecfunct()
gap.CompatibleConjugacyClasses(GGGG,ccl,tbl,recor)
CTBL=gap.CharacterTableWithStoredGroup(GGGG,tbl,recor)

After this last line (with CTBL=...) the error occurs. When I delete the lines between "# Hier Einschub..." and "# Hier Ende des Einschubs ", then the code works.

I would be grateful for any help.

Thanks in advance.

Thank you very much for your comment! :-)

Thank you very much for your answer! :-)

Dear SAGE team,

I would like to let MAGMA inside SAGE create a subgroup of a group (which was also created with MAGMA inside SAGE), but an error message was returned.

Unfortunately, I don't know ho to resolve this.

I would be thankful for any help.

Here's the code (only an example):

sage: GG=gap.SymmetricGroup(4)

sage: gensGG = gap.GeneratorsOfGroup(GG)

sage: m=gap.LargestMovedPoint(gensGG)

sage: GGG=magma.Sym(m)

sage: GG_MAGMA=magma.new('sub< GGG | [(1,2)] > ')

The error message is as follows:

TypeError Traceback (most recent call last) <ipython-input-13-da9ee2cf66f9> in <module>() ----> 1 GG_MAGMA=magma.new('sub<ggg|[(1,2)]&gt;')< p="">

/var/autofs/nfs/scratch/hannes/sage-8.8/local/lib/python2.7/site-packages/sage/interfaces/interface.pyc in new(self, code) 351 352 def new(self, code): --> 353 return self(code) 354 355 ###################################################################

/var/autofs/nfs/scratch/hannes/sage-8.8/local/lib/python2.7/site-packages/sage/interfaces/magma.pyc in __call__(self, x, gens) 792 pass 793 --> 794 A = Expect.__call__(self, x) 795 if has_cache: 796 x._magma_cache[self] = A

/var/autofs/nfs/scratch/hannes/sage-8.8/local/lib/python2.7/site-packages/sage/interfaces/interface.pyc in __call__(self, x, name) 286 287 if isinstance(x, string_types): --> 288 return cls(self, x, name=name) 289 try: 290 return self._coerce_from_special_method(x)

/var/autofs/nfs/scratch/hannes/sage-8.8/local/lib/python2.7/site-packages/sage/interfaces/expect.pyc in __init__(self, parent, value, is_name, name) 1441 except (RuntimeError, ValueError) as x: 1442 self._session_number = -1 -> 1443 raise_(TypeError, TypeError(*x.args), sys.exc_info()[2]) 1444 except BaseException: 1445 self._session_number = -1

/var/autofs/nfs/scratch/hannes/sage-8.8/local/lib/python2.7/site-packages/sage/interfaces/expect.pyc in __init__(self, parent, value, is_name, name) 1436 else: 1437 try: -> 1438 self._name = parent._create(value, name=name) 1439 # Convert ValueError and RuntimeError to TypeError for 1440 # coercion to work properly.

/var/autofs/nfs/scratch/hannes/sage-8.8/local/lib/python2.7/site-packages/sage/interfaces/interface.pyc in _create(self, value, name) 482 def _create(self, value, name=None): 483 name = self._next_var_name() if name is None else name --> 484 self.set(name, value) 485 return name 486

/var/autofs/nfs/scratch/hannes/sage-8.8/local/lib/python2.7/site-packages/sage/interfaces/magma.pyc in set(self, var, value) 627 13/5 628 """ --> 629 out = self.eval("%s:=%s" % (var, value)) 630 if out.lower().find("error") != -1: 631 raise TypeError("Error executing Magma code:\n%s" % out)

/var/autofs/nfs/scratch/hannes/sage-8.8/local/lib/python2.7/site-packages/sage/interfaces/magma.pyc in eval(self, x, strip, *kwds) 561 ans = Expect.eval(self, x, *kwds).replace('\\n', '') 562 if 'Runtime error' in ans or 'User error' in ans: --> 563 raise RuntimeError("Error evaluating Magma code.\nIN:%s\nOUT:%s" % (x, ans)) 564 return ans 565

TypeError: Error evaluating Magma code. IN:_sage_[3]:=sub<ggg|[(1,2)]&gt;; out:<="" p="">

_sage_[3]:=sub<ggg|[(1,2)]&gt;; ^="" user="" error:="" identifier="" 'ggg'="" has="" not="" been="" declared="" or="" assigned<="" p="">

Thank you very much for your answer! :-)

To whom it may concern: In the meantime I got to know that the following is also a possible solution (exemplarily done for G=$S_4$):

gap.LoadPackage('"ctbllib"')

ct=magma_free("G:=Sym(4);ct:=CharacterTable(G);ct;")

myfile=file("tbl_MAGMA.txt", 'w')

print >> myfile, ct

print >> myfile.close()

tbl=gap.GAPTableOfMagmaFile('"tbl_MAGMA.txt"', '"MAGMA_TBL"')

gap.Display(tbl)

G=gap.SymmetricGroup(4)

gap.ConnectGroupAndCharacterTable(G,tbl)

In the meantime I have learned that these things can be done for admissible quotients of path algebras with the aid of the GAP package QPA. This also works in Sage via letting GAP be the intermediator.

It works as follows:

gap> LoadPackage("qpa");;
gap> k:=Rationals;
Rationals
gap> Q:=Quiver(1,[[1,1,"a"],[1,1,"b"]]);
<quiver with 1 vertices and 2 arrows>
gap> kQ:=PathAlgebra(k,Q);
<Rationals[<quiver with 1 vertices and 2 arrows>]>
gap> AssignGeneratorVariables(kQ);
\#I  Assigned the global variables [ v1, a, b ]
gap> rels:=[a^2,b^2, a*b-b*a];
[ (1)*a^2, (1)*b^2, (1)*a*b+(-1)*b*a ]
gap> A:=kQ/rels;
<Rationals[<quiver with 1 vertices and 2 arrows>]/
<two-sided ideal in <Rationals[<quiver with 1 vertices and 2 arrows>]>, 
  (3 generators)>>
gap> IsAdmissibleQuotientOfPathAlgebra(A);
true
gap> RAD:=RadicalOfAlgebra(A);
<algebra of dimension 3 over Rationals>
gap> Display(RAD);
Algebra( Rationals, [ [(1)*a], [(1)*b], [(1)*a*b] ] )
gap> Dimension(RAD);
3
gap>

If we let $k$ be a finite field, then the command

IdempotentsForDecomposition(A);

works, but I don't have a computational solution for the case $k=\mathbb{Q}$. I do not yet have a solution for the non-commutative case.

Hi,

I'd like to ask the following:

I'd like to use SAGE in order to compute something with the free magma online calculator and then convert it into a GAP object. Unfortunately, there occurs an error, and I don't know, how to fix this. Any help is very much appreciated.

I followed the example on page 91 of http://www.math.rwth-aachen.de/~Thoma...

Here is what I did:

sage: gap.LoadPackage('"ctbllib"');
sage: ct=magma_free("G:=Alt(5);ct:=CharacterTable(G);ct;")
sage: tmpdir = gap.DirectoryTemporary()
sage: file=gap.Filename(tmpdir, '"magmatable"')
sage: gap.FileString(file,ct)
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-5-fd546564c72c> in <module>()
----> 1 gap.FileString(file,ct)

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/interface.pyc in __call__(self, *args, **kwds)
    627 
    628     def __call__(self, *args, **kwds):
--> 629         return self._parent.function_call(self._name, list(args), kwds)
    630 
    631     def _instancedoc_(self):

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/gap.pyc in function_call(self, function, args, kwds)
    921 
    922         """
--> 923         args, kwds = self._convert_args_kwds(args, kwds)
    924         self._check_valid_function_name(function)
    925 

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/interface.pyc in _convert_args_kwds(self, args, kwds)
    530         for i, arg in enumerate(args):
    531             if not isinstance(arg, InterfaceElement) or arg.parent() is not self:
--> 532                 args[i] = self(arg)
    533         for key, value in iteritems(kwds):
    534             if not isinstance(value, InterfaceElement) or value.parent() is not self:

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/interface.pyc in __call__(self, x, name)
    278 
    279         if isinstance(x, string_types):
--> 280             return cls(self, x, name=name)
    281         try:
    282             return self._coerce_from_special_method(x)

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/expect.pyc in __init__(self, parent, value, is_name, name)
   1443             except (RuntimeError, ValueError) as x:
   1444                 self._session_number = -1
-> 1445                 raise_(TypeError, TypeError(*x.args), sys.exc_info()[2])
   1446             except BaseException:
   1447                 self._session_number = -1

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/expect.pyc in __init__(self, parent, value, is_name, name)
   1438         else:
   1439             try:
-> 1440                 self._name = parent._create(value, name=name)
   1441             # Convert ValueError and RuntimeError to TypeError for
   1442             # coercion to work properly.

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/interface.pyc in _create(self, value, name)
    474     def _create(self, value, name=None):
    475         name = self._next_var_name() if name is None else name
--> 476         self.set(name, value)
    477         return name
    478 

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/gap.pyc in set(self, var, value)
   1387         """
   1388         cmd = ('%s:=%s;;' % (var, value)).replace('\n','')
-> 1389         self._eval_line(cmd, allow_use_file=True)
   1390 
   1391     def get(self, var, use_file=False):

/opt/sage/local/lib/python2.7/site-packages/sage/interfaces/gap.pyc in _eval_line(self, line, allow_use_file,         
wait_for_prompt, restart_if_needed)
    787                     return ''
    788             else:
--> 789                 raise RuntimeError(message)
    790 
    791         except KeyboardInterrupt:

TypeError: Gap terminated unexpectedly while reading in a large line:
Gap produced error output
Syntax error: ; expected in /home/boehmler/.sage/temp/mahlzahn/8255/interface/\
tmp8325 line 1
\$sage2:=Character Table of Group G-------------------------------------------\
----------Class |   1  2  3    4    5Size  |   1 15 20   12   12Order |   1  2\
  3    5    5---------------------------p  =  2   1  1  3    5    4p  =  3   1\
  2  1    5    4p  =  5   1  2  3    1    1---------------------------X.1   + \
  1  1  1    1    1X.2   +   3 -1  0   Z1 Z1#2X.3   +   3 -1  0 Z1#2   Z1X.4  \
 +   4  0  1   -1   -1X.5   +   5  1 -1    0    0Explanation of Character Valu\
e Symbols--------------------------------------# denotes algebraic conjugation\
, that is,#k indicates replacing the root of unity w by w^kZ1     = (Cyclotomi\
cField(5: Sparse := true)) ! [ RationalField() | 0, 0, -1, -1 ];;
                       ^

   executing Read("/home/boehmler/.sage/temp/mahlzahn/8255/interface/tmp8325");
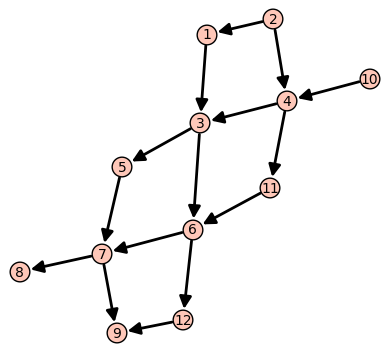
sage:

Hi,

I'd like to draw an Auslander-Reiten quiver with sage. I tried to do this by viewing the Auslander-Reiten quiver as a digraph, but, unfortunately, I was not able to find out how to let sage draw both dashed and solid arrows in one digraph.

Is this possible? If not, is there another way to let sage draw Auslander-Reiten quivers?

Any help would be appreciated.

Edit:

I used the following code:

sage: H=DiGraph()

sage: H.add_edges([(2,1),(2,4),(10,4),(1,3),(4,3),(4,11),(11,6),(3,6),(3,5),(5,7),(6,7),(6,12)])

sage: H.add_edges([(7,8),(7,9),(12,9)])

After having typed

sage: H.show()

a few times I got the following output:

Now, I'd like to draw dahed arrows indicating the Auslander-Reiten translates (e.g. a dashed arrow from 3 to 2).