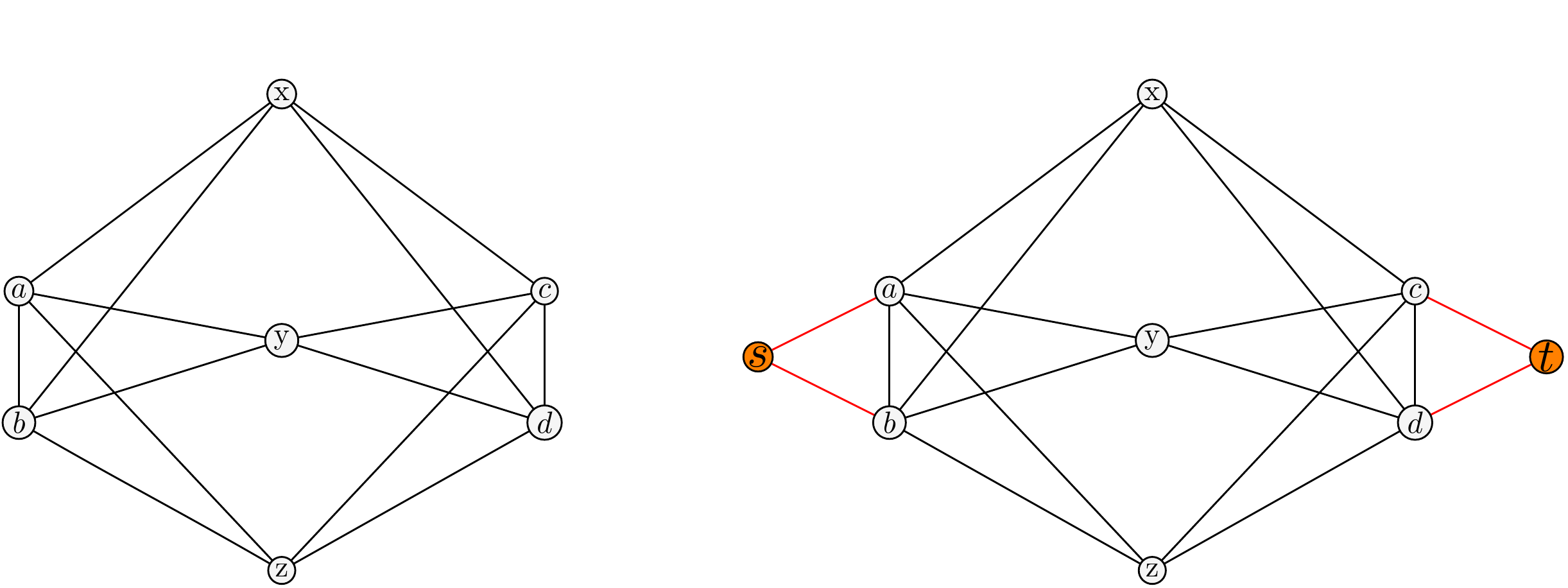
Let $A$ and $B$ be two proper subsets of the vertex set of a graph $G$.
An (A, B)-vertex separator is a set of vertices $S$ such that, after removing $S$ from the graph, there is no path from any vertex in $A$ to any vertex in $B$. A minimum (A, B)-vertex separator is such a set $S$ with the smallest possible size.
In sagemath, we have vertex_cut to return a minimum vertex cut between non-adjacent vertices 𝑠 and 𝑡.
My problem requires an extension of this functionality.
Similarly, it is also necessary to extend edge_cut, edge_disjoint_paths(), and vertex_disjoint_paths() from two vertices to two subsets.