Consider :
sage: var("x, y, rho, theta, k")
(x, y, rho, theta, k)
sage: g(rho, theta)=cos(theta)*exp(-rho^2)
sage: parametric_plot3d([rho*cos(theta), rho*sin(theta), g(rho, theta)], (rho, 0, 2), (theta, -pi, pi), aspect_ratio=[1, 1, 2], title="g").show(viewer="tachyon")
Launched png viewer for Graphics3d Object
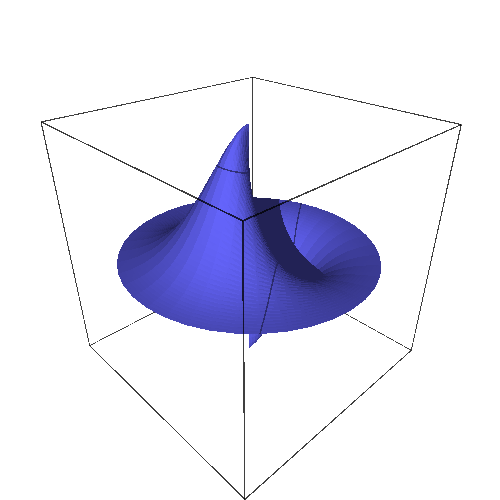
This function isn't even defined at the origin, nor it does have a limit stricto sensu. It has, however, a well defined directional limit, trivially computed :
sage: limit(g(rho, theta), rho=0)
cos(theta)
However, the very same limit is irretrievabl when expressed in Cartesian coordinates :
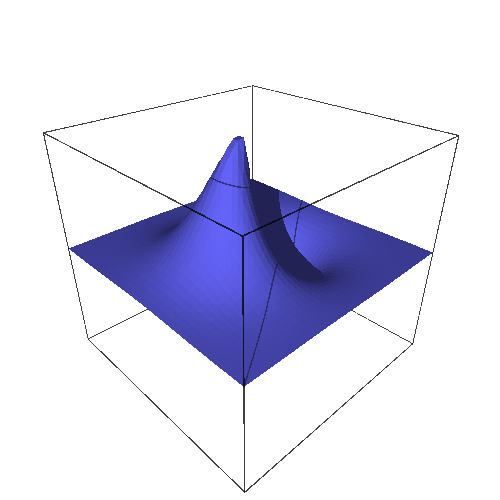
sage: f(x, y)=g(rho, theta).subs({rho^2:x^2+y^2, theta:atan2(y, x)}) ; f
(x, y) |--> x*e^(-x^2 - y^2)/sqrt(x^2 + y^2)
We can visually check that this function is the same as $g$ :
sage: plot3d(f(x, y), (x, -2, 2), (y, -2, 2), aspect_ratio=[1, 1, 2], title="f").show(viewer="tachyon")
Launched png viewer for Graphics3d Object
sage: f(x, y).subs({y:k*x}).limit(x=0)
ind
There are (at least) two ways to get a result :
sage: f(x, y).subs({y:k*x}).limit(x=0, taylor=True)
1/sqrt(k^2 + 1)
sage: f(x, y).subs({y:k*x}).limit(x=0, algorithm="sympy")
1/sqrt(k^2 + 1)
which is erroneous :
sage: f(x, y).subs({y:x*tan(theta)}).limit(x=0, algorithm="sympy")
sqrt(cos(theta)^2)
In fact, we expect $\cos\theta$ but we get $||\cos\theta||$. In other words, while the function is correctly computed, its directional limit loses its sign.
What am I doing wrong ?


