As there is no module about calculus of variations (or optimal control), I try to write the Euler equation from scratch
t, T, K_0, K_T, r=var('t T K_0 K_T r')
assume(r>0)
assume(K_0>0)
assume(K_T>0)
U=function('U')
Y=function('Y')
K=function('K')
K_t=function('K_t')
F=function('F')(t)
F(t)=e^(-r*t)*U(H(t))
F_t=function('F_t')
U_t=function("U'")(x)
F_t= diff(F,t)
H=function('H')
H(t) = r*K(t)-K_t(t)+Y(t)
show(LatexExpr(r'F(t) = '),F(t))
show(LatexExpr(r'\dot{F}(t) = '),F_t(t))
which gives
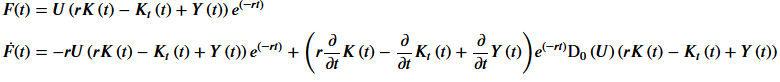
Here I encounter two difficulties :
1) I want substiute to $D_0(U)$ the standard notation for univariate derivative (that is $U^\prime()$). But, dispite all the good advices which are in the answer to my question https://ask.sagemath.org/question/7826/latex-typesetting-for-derivatives-like-g/ I cannot obtain any result.
2) I would like to substitute later to the unformall $U(x)$ the function $x^a$ (or any other admissible functon like $U(x) = log(x)$). Also I must also declare a function fo $Y(t)$.This time also I cannot obtain what I am searching for.
I am sincerely sorry to be so uneffective in fiding some solutions.


