Hi
Sagemath9.7 Ubuntu22.04 in WSL2 W11
It's seems there is a problem with the function .alexander_polynomial()
The function never stops in this case:
#b0=[4, 5, 2, -4]
b1=[5, 6, 3, -5, 1]
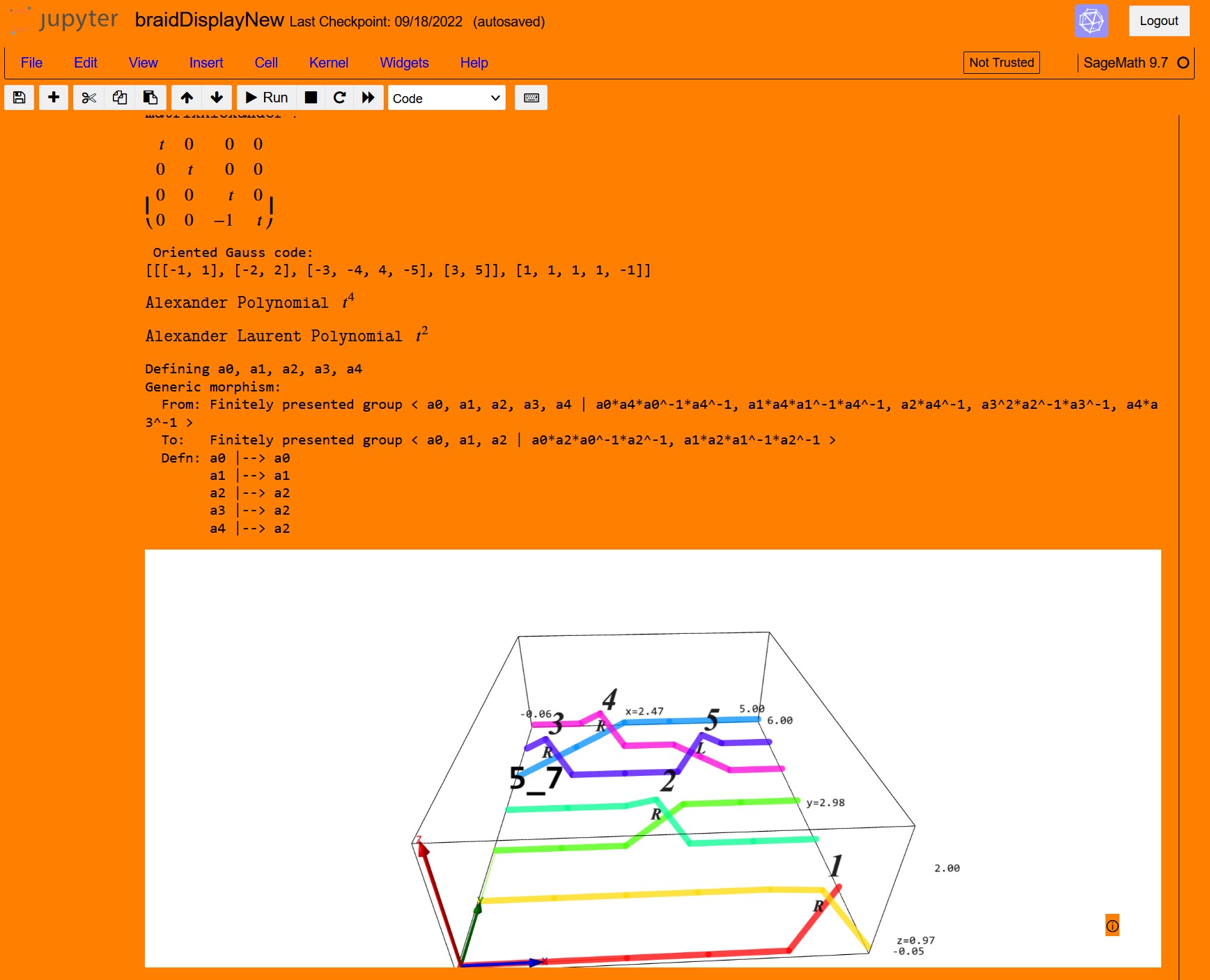
oGc=[[[-1, 1], [-2, 2], [-3, -4, 4, -5], [3, 5]], [1, 1, 1, 1, -1]] #
oGcKnot=Link(oGc)
oGcKnotPlt=plot(oGcKnot,axes=False)
show(oGcKnotPlt)
oGcKnot.alexander_polynomial()
#oGcKnot.jones_polynomial()
[edited 30/09/2022]
the problem seems that the function does not support an unknot with several crossings.crossings.
if you uncomment last line of the code below , it 's never stop
def addMirOrGauss(k0,k1,miror) :
""" link K0 with k1 """
if miror==True :
k1=k1.mirror_image()
#show("k0 ogc :\t ", k0.oriented_gauss_code())
#show("k1 ogc :\t ", k1.oriented_gauss_code())
nbCrossk0=len(k0.oriented_gauss_code()[-1])
oGck0k1=[[k0.oriented_gauss_code()[0][0]+[ (abs(el)+nbCrossk0)*sign(el) for el in k1.oriented_gauss_code()[0][0]]],
k0.oriented_gauss_code()[-1] + k1.oriented_gauss_code()[-1]]
#show("k0k1 OGC :\t",oGck0k1)
return oGck0k1
B0=BraidGroup(2)
b0=B0([1])
b0K=Link(b0)
oGcb0K=b0K.oriented_gauss_code()
alexPolyb0K= b0K.alexander_polynomial()
B1=BraidGroup(4)
b1=B1([ 3])
b1K=Link(b1)
oGcb1K=b1K.oriented_gauss_code()
alexPolyb1K= b1K.alexander_polynomial()
show(plot(b0))
show(plot(b1))
print('oGcb0K : ',oGcb0K)
print('b0 alexander_polynomial : ', alexPolyb0K)
print('oGcb1K : ',oGcb1K)
print('b1 alexander_polynomial : ', alexPolyb1K)
oGck0k1=addMirOrGauss(b0K,b1K,False)
b0b1K=Link(oGck0k1)
print('sum of k0 and k1 oGck0k1 Gauss Oriented code : ',oGck0k1 )
show(plot(b0b1K,axes=False))
#b0b1K.alexander_polynomial()


