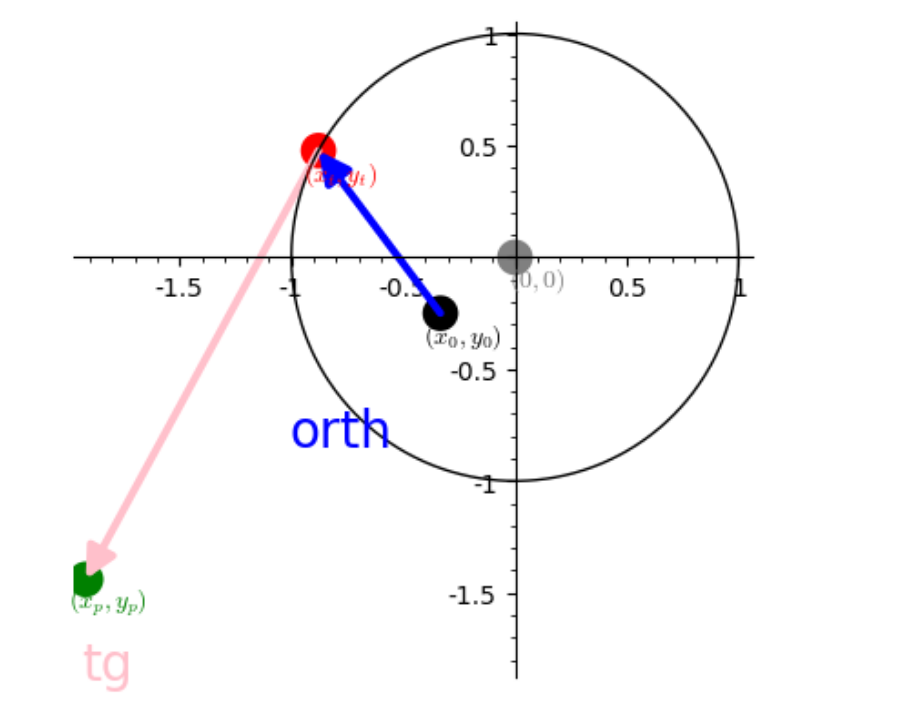
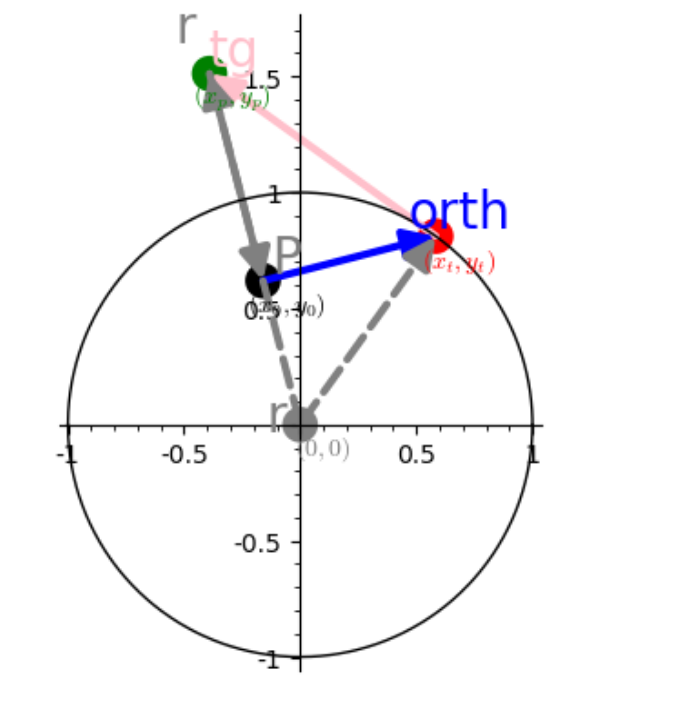
HI
why do i have to square the two terms of the equation so that solve gives me the solution?
why it does not alow him to do square both sides ?
vL=['x','y','r','x_0','y_0','x_p','y_p','x_t','y_t','atg','btg','alpha']
varL=var(vL)
x_0Num=-1/3 ;y_0Num=-1/4 ;rNum=1
numL=[x_0==x_0Num ,y_0==y_0Num ,r==rNum]
assume(x,'real')
assume(abs(x_0)<1)
assume(abs(y_0)<1)
assume(r>=1)
C_u(x)= sqrt(r^2-x^2)
C_d(x)= -sqrt(r^2-x^2)
delta_0(x)=y_0/x_0*x # radial to circle
delta_p(x)=-x_0/y_0*x + y_0+(x_0^2)/y_0 #perpendicular to circle radial delta_0
assume(delta_p>0)
# numerical solution
SupNum=solve((C_u(x)==delta_p(x)).substitute(numL), x, to_poly_solve=True)
# literal solutions which do not work
SupLit1=solve(C_u(x)== delta_p(x), x, to_poly_solve=True)
SupLit2=solve(C_u(x)== delta_p(x), x, algorithm='sympy')
# literal solutions ok
SupLit3=solve(C_u(x)^2== (delta_p(x))^2, x, algorithm='sympy')
SupLit4=solve(C_u(x)^2== (delta_p(x))^2, x, to_poly_solve=True)
show("Sup num : ",SupNum)
show("Sup lit 1 : ", LatexExpr(r" \huge \color{red} {?? }"),SupLit1)
show("Sup lit 2 : ", LatexExpr(r" \huge \color{red} {?? }"),SupLit2)
show("Sup lit 3 : ",SupLit3, LatexExpr(r" \huge \color{green} {OK }"))
show("Sup lit 4 : ",SupLit4, LatexExpr(r" \huge \color{green} {OK }"))