Hi
this exercise comes from a MOOC course that has just ended EDX.org , MITx: 6.431x Probability - The Science of Uncertainty and Data
forget()
var('pi_1 pi_2 pi_3 pi_4 pi_5 pi_6 pi_7 pi_8 pi_9')
# matrix of the Markov's Chain
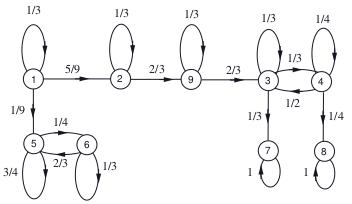
m = matrix([ \
[1/3 , 5/9 , 0 , 0 , 1/9 , 0 , 0 , 0 , 0 ], \
[ 0 , 1/3 , 0 , 0 , 0 , 0 , 0 , 0 , 2/3 ], \
[ 0 , 0 , 1/3 , 1/3 , 0 , 0 , 1/3 , 0 , 0 ], \
[ 0 , 0 , 1/2 , 1/4 , 0 , 0 , 0 , 1/4 , 0 ], \
[ 0 , 0 , 0 , 0 , 3/4 , 1/4 , 0 , 0 , 0 ], \
[ 0 , 0 , 0 , 0 , 2/3 , 1/3 , 0 , 0 , 0 ], \
[ 0 , 0 , 0 , 0 , 0 , 0 , 1 , 0 , 0 ], \
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 1 , 0 ], \
[ 0 , 0 , 2/3 , 0 , 0 , 0 , 0 , 0 , 1/3 ] \
])
v=vector([pi_1,pi_2,pi_3,pi_4,pi_5,pi_6,pi_7,pi_8,pi_9])
#Assuming that the Markov chain is initially in state 2 (i.e., X0=2),
# what is the probability that the chain eventually reaches state 7?
#################################
# brute force
#x_0=2
v_s=vector([0,1,0,0,0,0,0,0,0])
#v_s=vector([0,0,1,0,0,0,0,0,0])
V_r=v_s*m^110
show(V_r[6].n())
#################################
# smart way
eqT=[]
for i in range(0,len(v)):
eqT.append(m[i]*v==v[i])
show(eqT[2])
show(eqT[3])
S=solve([eqT[2],eqT[3],pi_7==1,pi_8==0],pi_3,pi_4,pi_7,pi_8)
show(S)
show("probability that the chain eventually reaches state 7 : ",S[0][0])
I would like to generate the variables, and the vector automaticaly: kind of:
dimM=m.dimensions()[1]
varStr=''
for i in range(0,dimM):
#varStr=varStr+ ' a_'+str(i+1)
varStr=varStr+ ' a_'+str(i)
show(varStr)
var(varStr)
R = PolynomialRing(QQ, dimM, 'a_')
v= vector(R,dimM, R.gens())
show(m)
show(v)
eqT=[]
for i in range(0,len(v)):
show(m[i]*v==v[i])
eqT.append(m[i]*v==v[i])
#show(eqT)
but unfortunately this code just above for generating variables and vector automaticaly does not work

