 | 1 | initial version |
Basically I have a function that needs to access "external" but constant values. For example, simplified:
The as are constant but I don't know n beforehand. My goal is to use SAGE to calculate the integral and derivative of a larger function. I know that there is a symbolic sum function, but I am not sure if it is possible to use the index to refer to something undefined and "external" to the function.
| | 2 | No.2 Revision |
Basically I have a function that needs to access "external" but constant values. For example, simplified:
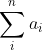
The as are constant but I don't know n beforehand. My goal is to use SAGE to calculate the integral and derivative of a larger function. I know that there is a symbolic sum function, but I am not sure if it is possible to use the index to refer to something undefined and "external" to the function.
By now I have stumbled over the function ... function which I misuse to serve my purpose (can I link a sagecloud notebook here?):
%var x, y, z, i, n
ai = function('ai')
xi = function('xi')
yi = function('yi')
zi = function('zi')
gauss(a,x,y,z) = a * e^(-(x^2+y^2+z^2)/2)
f(x,y,z) = (sum( gauss(ai(i),x-xi(i), y-yi(i), z-zi(i)) ,i,1,n))^2
integral(integral(integral(f,x),y),z)
Which results in:
(x, y, z) |--> integrate(integrate(integrate(sum(ai(i)*e^(-1/2*x^2 - 1/2*y^2 - 1/2*z^2 + x*xi(i) - 1/2*xi(i)^2 + y*yi(i) - 1/2*yi(i)^2 + z*zi(i) - 1/2*zi(i)^2), i, 1, n)^2, x), y), z)
Does this mean SAGE is not able to integrate this symbolically?
Copyright Sage, 2010. Some rights reserved under creative commons license. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.