Hi,
I would like to compute the volume V of the lower polyhedron (that does not contain vertex A) let's call it $poly_G$. (let's call $poly_A$ the upper polyhedron that does not contain G). Size is $a=AB=BF=...$
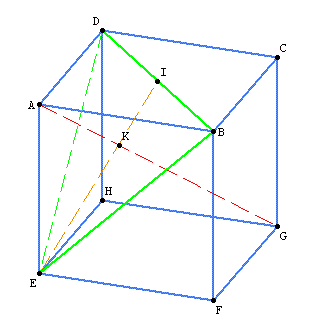
We can compute using Pythagore's theorem and median's properties by introducing K and I points. I can do that by hand.
I want to compute the volume with sage, I have tried this sage using volume integrations but I am not sure about the result at all... I look for the plane DBE normal which gives its equation $x-y+z$. Then I compute using triple integrations.
c = cube(center=(0.5,0.5,0.5))
x=var('x')
y=var('y')
z=var('z')
a=var('a')
u=vector([a,a,0])
v=vector([0,a,a])
print u.cross_product(v)
intz = integrate(1,z,0,a-y-x)
inty = integrate(intz,y,0,a-x)
intx = integrate(inty,x,0,a)
print intx
I would like to know if there are elegant ways of computing this kind of problem in sage ? And in addition, if this require few lines, how can I display the above figure ? Sorry if this looks simple, I am new to Sage.
Thanks,

