contour_plot behaves differently when I include the functional dependence

edit

If I include the functional dependence of my function, the contour_plot routine behaves differently. MWE:

var('x y')
def check(x,y):
    val=-1. # negative by default, 
    for j in range(1,10): 
        for i in range(1,10): 
            if ( ( (x>0.9*i) and (x<1.1*i) ) and ( (y>0.9*j) and (y<1.1*j) ) ):
                val=1.
    return val

So this is kind of a strange function, but basically if (x,y) are near any of the 2d grid points (1-10), the function is 1 instead of zero. If I call this function without specifying the functional dependence, it looks right:

contour_plot(check,(x,-1.,8.),(y,-1.,8.))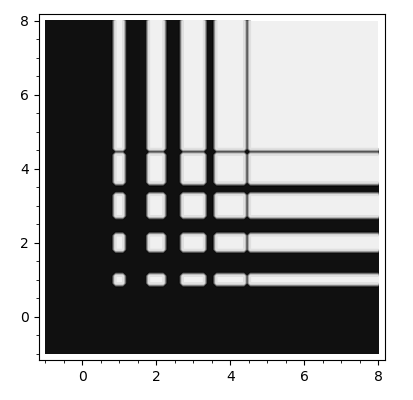

However, if I call them and specify them explicitly, I get the unexpected (to me):

contour_plot(check(x,y),(x,-1.,8.),(y,-1.,8.))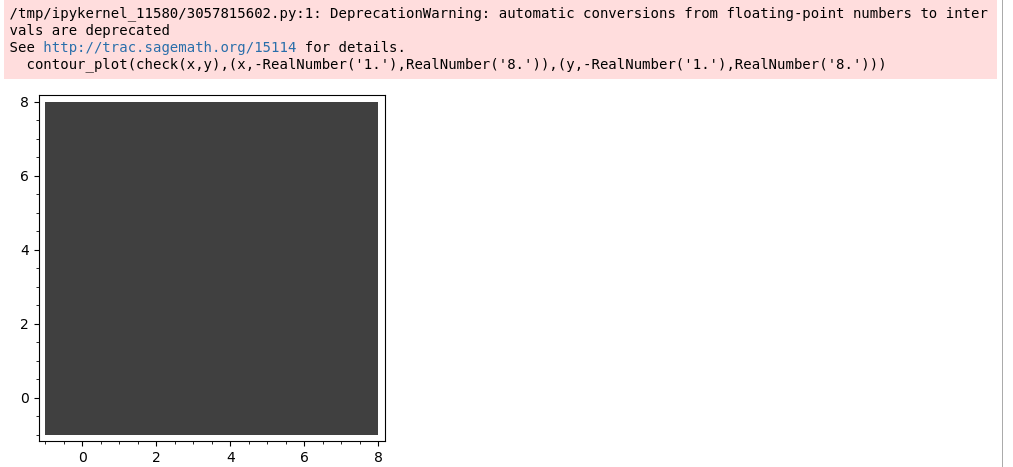

(I grabbed the depreciation warning too, although I don't see how it matters here).

This is not just academic, because what I really want to do is have a four-variable funcftion, a la

def h(x,y,z,w):
...

and do a contour plot on two variables, setting the other two constant, like

contour_plot(h(x,y,0,1),....)

I'm having trouble, and trying to debug. Any thoughts?