subgraph_search_iterator gives duplicate subgraphs

edit

I use subgraph_search_iterator to obtain all the subgraphs isomorphic to $H$ of a graph $G$. However, in the following example, I found that many obtained subgraphs appear to be duplicates, which surprises me. Have I misunderstood this function?

G=graphs.OctahedralGraph()
H = graphs.CycleGraph(3)
L = list(G.subgraph_search_iterator(H, induced=False,return_graphs=False)) 
len(L)

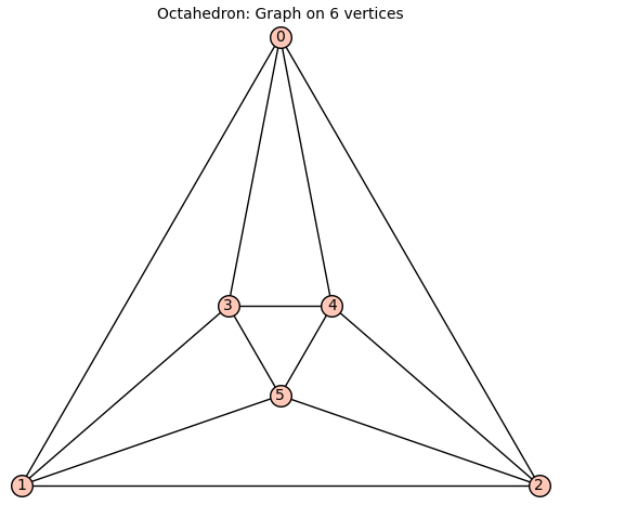
L[1]
L[4]
L[18]

We will see that the 3-cycle formed by vertices 0, 1, and 3 appears three times. What could be the reason for this? How can we avoid such occurrences?

Edits: In fact, the 3-cycle formed by vertices 0, 1, and 3 appears six times.

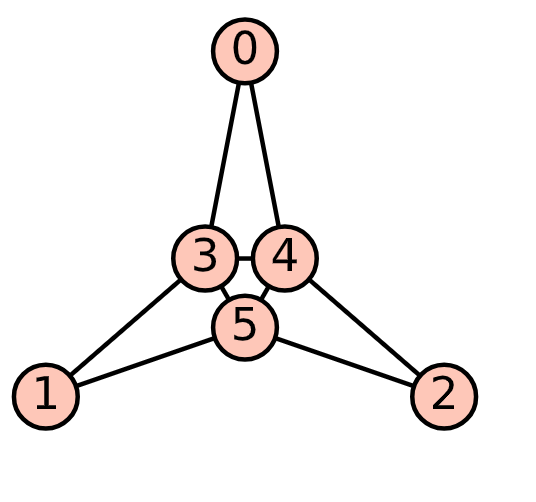
Perhaps the $C_3$ are too specific and overshadowing something. If we consider the following example, we will discover that $H$ appears as many times as the number of copies of H without labels multiplied by the order of automorphisms of $H$. (label $H$ ?)

G=graphs.OctahedralGraph()
H=copy(G)
H.delete_edges( [(0,1), (1,2), ( 0,2 )])
print( sum(1 for _ in G.subgraph_search_iterator(H, induced=False,return_graphs=False) ) )
L = { tuple(g.edges(labels=False,sort_vertices=True,sort=True)) for g in G.subgraph_search_iterator(H, induced=False) }
print(len(L))
H.automorphism_group( ).order( )

48
8
6