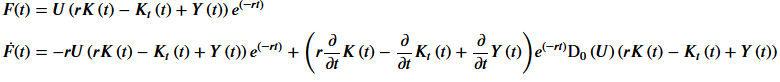First : as given, your code does not run, some functions being used before definition. Please do your homework and check your sample code after reset()ting before posting.
Your problem is that the operator of a derivative expression is not recognized as a function by substitute_function. After running :
t, T, K_0, K_T, r=var('t T K_0 K_T r')
assume(r>0)
assume(K_0>0)
assume(K_T>0)
U=function('U')
Y=function('Y')
K=function('K')
K_t=function('K_t')
# H=function('H') # Superfluous, ,since H is defined immediately below
H(t) = r*K(t)-K_t(t)+Y(t) # H must be defined fefore being used in F(t)
# F=function('F')(t) # Superfluous, ,since F is defined immediately below
F(t)=e^(-r*t)*U(H(t))
# F_t=function('F_t') # Superfluous, since f_t is defined two lines below.
# U_t=function("U'")(x)
U_t=function("U'")
F_t= diff(F,t)
We can ask :
view(LatexExpr("F(t)=%s"%latex(F(t))))
which displays :
$$ \dot{F}(t)=U\left(r K\left(t\right) - K_{t}\left(t\right) + Y\left(t\right)\right) e^{\left(-r t\right)} $$
The expression to be reexpressed is
sage: foo=F_t(t).maxima_methods().part(1,1) ; foo
D[0](U)(r*K(t) - K_t(t) + Y(t))
(This site's Mathjax isn't able to typeset this, bur LeTeX can).
Whose operator (= function) is
sage: foo.operator()
D[0](U)
We should be able to write :
F_t().substitute_function(F_t(t).maxima_methods().part(1,1).operator(), U_t)
But this does not work, this operator being not recognized as a function :
sage: F_t().substitute_function(F_t(t).maxima_methods().part(1,1).operator(), U_t)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In [256], line 1
----> 1 F_t().substitute_function(F_t(t).maxima_methods().part(Integer(1),Integer(1)).operator(), U_t)
File /usr/local/sage-10/src/sage/symbolic/expression.pyx:6063, in sage.symbolic.expression.Expression.substitute_function()
6061 else:
6062 for a in args:
-> 6063 _dict_update_check_duplicate(sdict, _subs_fun_make_dict(a))
6064
6065 if kwds:
File /usr/local/sage-10/src/sage/symbolic/expression.pyx:724, in sage.symbolic.expression._subs_fun_make_dict()
722 else:
723 msg = "not able to determine a substitution from {}"
--> 724 raise TypeError(msg.format(s))
725
726
TypeError: not able to determine a substitution from D[0](U)
The key is that :
sage: foo.operator() in SR
False
Complain fiercely. Or file a well-documented issue...
The workaround is to replace the whole subexpression foo in the expression you want to reformat, which gives :
view(LatexExpr(r"\dot{F}(t)=%s"%latex(F_t(t).subs({foo:U_t(*foo.operands())}))))
$$ \dot{F}(t)=-r U\left(r K\left(t\right) - K_{t}\left(t\right) + Y\left(t\right)\right) e^{\left(-r t\right)} + {\left(r \frac{\partial}{\partial t}K\left(t\right) - \frac{\partial}{\partial t}K_{t}\left(t\right) + \frac{\partial}{\partial t}Y\left(t\right)\right)} {\rm U'}\left(r K\left(t\right) - K_{t}\left(t\right) + Y\left(t\right)\right) e^{\left(-r t\right)} $$
For your second qyuuestion the substitution has no role, because you can substitute U before differentiating ; no further derivative ioerators in sight :
sage: F(t).substitute_function(U, (x^a).function(x)).diff(t)
(r*diff(K(t), t) - diff(K_t(t), t) + diff(Y(t), t))*(r*K(t) - K_t(t) + Y(t))^(a - 1)*a*e^(-r*t) - (r*K(t) - K_t(t) + Y(t))^a*r*e^(-r*t)
$$ -r e^{\left(-r t\right)} \log\left(r K\left(t\right) - K_{t}\left(t\right) + Y\left(t\right)\right) + \frac{{\left(r \frac{\partial}{\partial t}K\left(t\right) - \frac{\partial}{\partial t}K_{t}\left(t\right) + \frac{\partial}{\partial t}Y\left(t\right)\right)} e^{\left(-r t\right)}}{r K\left(t\right) - K_{t}\left(t\right) + Y\left(t\right)}
$$
sage: a=SR.var("a")
sage: F(t).substitute_function(U, (x^a).function(x)).diff(t)
(r*diff(K(t), t) - diff(K_t(t), t) + diff(Y(t), t))*(r*K(t) - K_t(t) + Y(t))^(a - 1)*a*e^(-r*t) - (r*K(t) - K_t(t) + Y(t))^a*r*e^(-r*t)
$$ {\left(r \frac{\partial}{\partial t}K\left(t\right) - \frac{\partial}{\partial t}K_{t}\left(t\right) + \frac{\partial}{\partial t}Y\left(t\right)\right)} {\left(r K\left(t\right) - K_{t}\left(t\right) + Y\left(t\right)\right)}^{a - 1} a e^{\left(-r t\right)} - {\left(r K\left(t\right) - K_{t}\left(t\right) + Y\left(t\right)\right)}^{a} r e^{\left(-r t\right)}
$$
HTH,