A last factorization

edit

Sorry for all, but one more time I fail to go to the last factorization. The following code

varx=var('x y') 
paramu=var('A α β U')
paramuc=tuple(list(paramu)+[U])
paramb=var('R p_x p_y')
varl=var('λ')
varg=tuple(list(varx)+[λ])
assume(x>=0)
assume(y>=0)
assume(p_x>0)
assume(p_y>0)
assume(A>0)
assume(α>0)
assume(α<1)
assume(β>0)
assume(β<1)
def Cobb_Douglas(x, y, A, α, β) :
    return A*x^α*y^β

def expense(x,y,p_x,p_y) :
    return p_x*x+ p_y*y

L(x,y,λ) = Cobb_Douglas(x,y,A, α, β) -λ*(expense(x,y,p_x,p_y)-R)
M=det(L.hessian()(x,y,λ)).full_simplify().factor().collect_common_factors()
show(M)

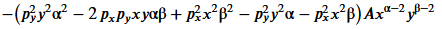
But it is obvious that we can factor it in such a way to finaly obtain

$-(p_y^2 y^2 \alpha (\alpha-1)+ p_x^2 x^2 \beta (\beta-1) - 2 p_x p_y x y \alpha \beta) Ax^{\alpha-2}y^{\beta-2}$

Under this last factorization, it is obvious that according to the assumptions this last expression should be signed but which ever the question I ask with bool() the answer is False.