Solve inequation composed of FractionFieldElement

edit

As in your previous question, the lhs() of your inequation $\left(\frac{x^2}{x+1}\right)$ is not a polynomial.

And the solution proposed by Sage :

sage: solve_ineq(x^2/(x+1)>=0, x)
[[x > -1]]

is correct :

• such an inequation has meaning only for real values ;

• $x$ being a real, $x^2$ is non-negative ; therefore, $\frac{x^2}{x+1}$ has the sign of $x+1$, which is

  • positive for $x>-1$ (except for $x=0$, where your lhs() is zero),
  • negative for $x<-1$, and
  • indeterminate for $x=-1$.

These cases exhaust the possibilities for $x\in\mathbb{R}$.

Now, your inequation may be meaningful if $x$ is a non-real complex with the added constraint $\displaystyle\frac{x^2}{x+1}\in\mathbb{R}$. This constraint can be implemented as (x^2/(x+1)).imag()==0. Rewriting $x=a+i\,b$, we get :

sage: var("a, b", domain="real")
(a, b)
sage: solve_ineq([(x^2/(x+1)).subs(x==a+I*b).imag()==0, (x^2/(x+1)).subs(x==a+I*b)>=0], [b])
[[b == I*a, 1 != 0, 2*a == 0, 2*a + 1 != 0],
 [b == 0, a + 1 != 0, a^2 + 2*a + 1 != 0, a],
 [a + I*b + 1 > 0,
  a + I*b != 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, a + 1 > 0, a != 0, a^2 + 2*a + 1 != 0],
 [-a - I*b - 1 > 0,
  -(a + I*b)^2 > 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, -a - 1 > 0, -a^2 > 0, a^2 + 2*a + 1 != 0]]

• The first case boils down to $x=0$ ;
• the second to $x\neq-1$ (and misses the positivity constraint) ;
• the third is meaningless/impossible for $a, b\in\mathbb{R}$ (except for $a=b=0$, which it excludes) ;
• the fourth is identical to the second ;
• the fifth leads to the same conclusions than the third ;
• the sixth is impossible.

Sage's solve_ineq can't find the solutions (if any exists) of this form. This might deserve further exploration, with more advanced techniques (think algebraic geometry...).

EDIT : In this special case, the solution set can be computed "by hand" by rewriting $\frac{x^2}{x+1}$ as $a+i\,b$, solving $\frac{x^2}{x+1}\in\mathbb{R}$ (by solving $\Im\left(\frac{x^2}{x+1}\right)=0$) for $b$, and substituting each of these solutions to solve $\Re\left(\frac{x^2}{x+1}\right)>=0$ for $a$ :

sage: ExR=(x^2/(x+1)).subs(x==a+I*b) ; ExR
(a + I*b)^2/(a + I*b + 1)
sage: Sb=ExR.imag().factor().solve(b) ; Sb
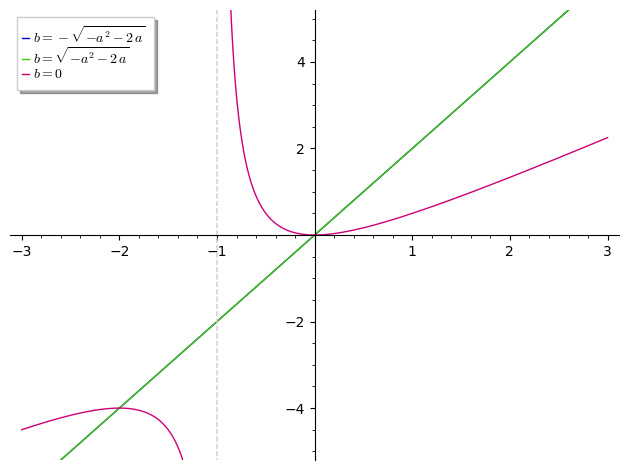
[b == -sqrt(-a^2 - 2*a), b == sqrt(-a^2 - 2*a), b == 0]
sage: {u:solve_ineq(ExR.real().factor().subs(u)>=0, a) for u in Sb}
{b == -sqrt(-a^2 - 2*a): [[a >= 0]],
 b == sqrt(-a^2 - 2*a): [[a >= 0]],
 b == 0: [[a > -1]]}

Illustration :

sage: plot([ExR.real().factor().subs(u) for u in Sb], (a, -3, 3), ymin=-5, ymax=5, legend_label=["$%s$"%latex(u) for u in Sb], detect_poles="show")
Launched png viewer for Graphics object consisting of 5 graphics primitives

HTH,