Finding all non-isomorphic $C_5$-free connected planar graphs of order 11.
Let us say that a graph is $H$-free if it does not contain $H$ as a subgraph (whether induced or not). We denote $C_5$ as a cycle with 5 vertices. Then I would like to find all the $C_5$ free planar connected graphs of order 11. (I can't estimate the number of them, hope it's not too many.) I tried to write the following code.
def C5free(g):
test=not graphs.CycleGraph(5).is_subgraph(g,induced=False)
return test
First, to check that the code will be executed correctly, I tried to filter out the 6 vertex $C_5$ free connected planar graphs. But the following code does not seem to filter the desired ones very well. Because 179 is the total number.
g6a=[g for g in graphs.planar_graphs(6,minimum_connectivity=1) if C5free(g)==True];
len(g6a) #179
g6b=[g for g in graphs.planar_graphs(6,minimum_connectivity=1)];
len(g6b) #179
However, obviously the graph with 6 vertices below is not $C_5$-free.
g=Graph([(0,1),(1,2),(2,3),(3,4),(4,0),(0,5)])
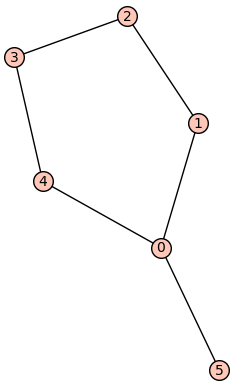
In addition, among these graphs, there may be some graphs being isomorphic to each other. Because we can see from the sequence about conencted planar graphs from https://oeis.org/A003094/list. It tells us that 99 is the number of non-isomorphic connected planar graphs on 6 vertices.

