Tree representing an expression

edit

Sage does not provide a built-in function for that.

However, such a function is given in the answer to this Sage question:

• Ask Sage question 9614: Getting a rooted graph from a nested list of lists

Refreshing the code from that answer for Python 3:

class ExpressionGraph():
    def __init__(self, expr):
        self.G = Graph()
        self.i = 0
        self.expr = expr
        self.root = None
        self.graph_expr(self.expr)
    def plot(self, *args, **kwds):
        # print "root is {0}".format(self.root)
        return self.G.plot(*args, layout='tree', tree_root=self.root, **kwds)
    def graph_expr(self, expr):
        try:
            operator = expr.operator()
        except AttributeError:  # e.g. if expr is an integer
            operator = None
        if operator is None:
            name = "[{0}] {1}".format(self.i, expr)
            # print(self.i)
            # print("(leaf) {0}".format(expr))
            self.i += 1
            self.G.add_vertex(name)
            return name
        else:
            name = "[{0}] {1}".format(self.i, expr.operator().__name__)
            # print(self.i)
            # print("(node) {0}; {1}".format(expr, expr.operator().__name__))
            if self.i == 0:
                self.root = name
                # print("  ** root is '{0}' **".format(self.root))
            self.i += 1
            new_nodes = []
            for opnd in expr.operands():
                new_nodes += [self.graph_expr(opnd)]
            self.G.add_vertex(name)
            self.G.add_edges([(name, node) for node in new_nodes])
            return name

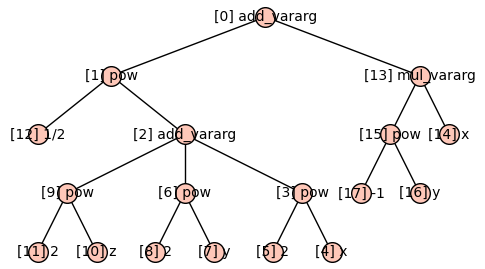
Using it:

sage: x, y, z = SR.var('x, y, z')
sage: f = sqrt(x^2+y^2+z^2) + x/y
sage: E = ExpressionGraph(f)
sage: E.plot()