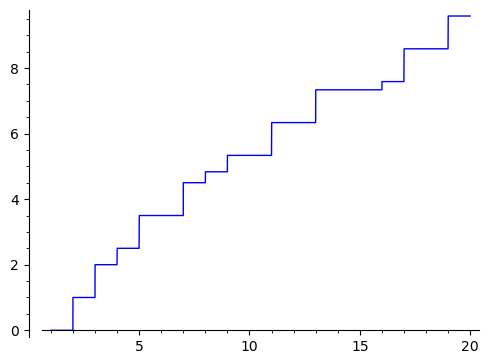
cannot convert log(x)/log(2) to int
If I define J(x) function as:
def J(x):
sum = 0
print(int(log(x)/log(2)))
for i in range(1, int(log(x)/log(2)) + 1):
sum = sum + 1 / i * prime_pi(x**(1/i))
return(N(sum))
when I try to plot it using:
p = plot(J(x), (x, 1, 20))
show(p)
I get the message:
cannot convert log(x)/log(2) to int
but if try J function acting on any float number I get a perfect value like:
sage: J(123.456789)
34.0333333333333
I have tried to replace int by floor but with the same result. Any help to solve the plotting problem will be welcome. Thank you.