How to solve a Bernoulli Diff EQ?

edit

[ I suppose that this is not homework. If it is, you should abstain from using my answer and find yourself your solution... ]

The x unknown of the D. E. is a function, so we'd better declare and use it as such :

sage: x=function("x")
sage: var("t")
t
sage: de=diff(x(t),t)==2*x(t)*(15-x(t))

Maxima (Sage's default DE solver) doesn't give an explicit answer :

sage: SM=desolve(de, x(t), ivar=t, contrib_ode=True) ; SM
-1/30*log(x(t) - 15) + 1/30*log(x(t)) == _C + t

Sympy does give an implicit answer :

sage: from sympy import dsolve, sympify
sage: SS=dsolve(*map(sympify, (de, x(t))))._sage_() ; SS
x(t) == 15/(C1*e^(-30*t) + 1)

Declare the integration constant and check the solution :

sage: var("C1")
C1
sage: bool(de.substitute_function(x, SS.rhs().function(t)))
True

Solve C1 for your boundary conditions :

sage: SC1=C1.subs(t==0).subs(x(0)==0).solve(C1) ; SC1
[C1 == 0]

The solution of your problem is therefore :

sage: SS.subs(SC1)
x(t) == 15

Your proposed solution:

sage: Px=(30*e^(30*t))/(1+2*e^(30*t)).function(t) ; Px
t |--> 30*e^(30*t)/(2*e^(30*t) + 1)

does not fulfill your boundary condition :

sage: Px(0)
10

BTW :

sage: limit(Px(t),t=oo)
15
sage: limit(Px(t),t=-oo)
0
sage: Px.plot((-5, 5))
Launched png viewer for Graphics object consisting of 1 graphics primitive

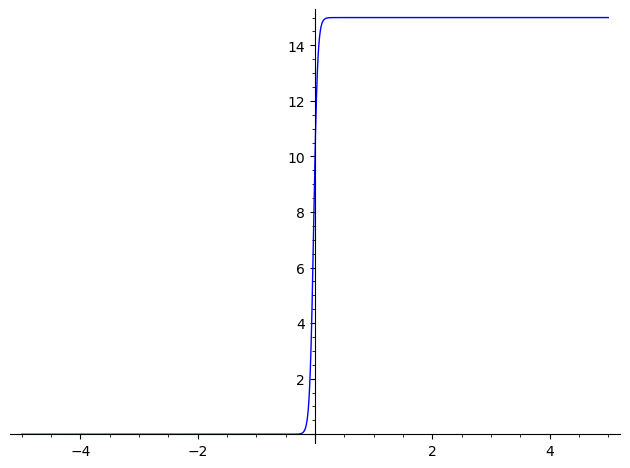
In other words, your proposed solution is a sigmoïd...

HTH,

EDIT : Maxima's solution can be exploited with a little "manual" work :

sage: S0=desolve(de, x(t)) ; S0
-1/30*log(x(t) - 15) + 1/30*log(x(t)) == _C + t

Let's declare the arbitrary constant :

sage: var("_C")
_C

log properties allow us to reshape this solution and solve it explicitly for x(t) :

sage: S1=(S0*30).simplify_log().solve(x(t)) ; S1
[x(t) == 15*e^(30*_C + 30*t)/(e^(30*_C + 30*t) - 1)]

which can be itself rewritten :

sage: var("a, b")
(a, b)
sage: w0,w1=(SR.wild(u) for u in range(2))
sage: S1t=[u.subs((b*(a/(a-1))==b*(1+1/(a-1))).subs(a==w0, b==w1)) for u in E1.solve(x(t))] ; S1t
[x(t) == 15/(e^(30*_C + 30*t) - 1) + 15]

This singleton solution checks the differential equation :

sage: [bool(de.substitute_function(x,u.rhs().function(t))) for u in S1t]
[True]

Is there a value of _C satisfying the boundary condition ?

sage: S2=S1[0].subs(t==0).subs(x(0)==15) ; S2
15 == 15*e^(-30*_C) + 15

Nope : e^(-30*_C) is nozero for all _C complexes.

It should be noted that Maxima's solution does not describe the "special case x(t)=15, which is a solution of de :

sage: de.substitute_function(x,SR(15).function(t))
0 == 0

HTH,

Be careful and make multiplication explicit.

The differential equation studied here is $$ x'(t) = 2 · x(t) · (15 - x(t)) $$ and not $$ x'(t) = 2 · x(15 - x(t)) $$ so instead of

de = diff(x, t) == 2 * x(15 - x)

you want

de = diff(x, t) == 2 * x * (15 - x)