limit of fourier series

savecancel

I'd like to compute the limit of $$\sum_{k=1}^{n}\frac{1}{k^2+1}\sin(kx)$$ I did the following already:

def b(k):
        return(1/(k**2+1))
def a(k,x):
        return(b(k)*sin(k*x))
def s(n,x):
        s=0 
        for k in range(1,n+1):
                s=s+a(k,x)
        return(s)
var('x,n')
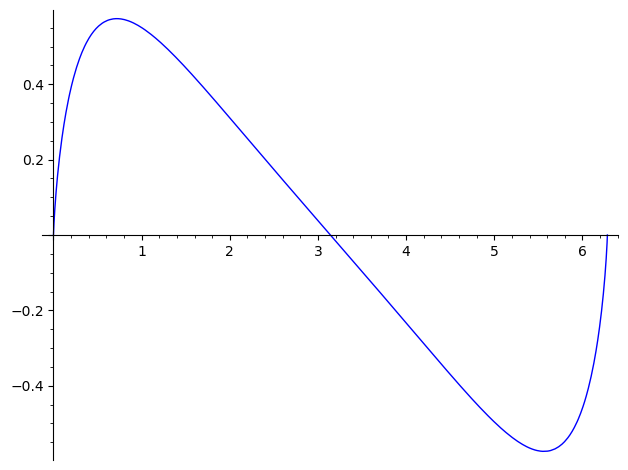
f=s(1000,x)
plot(f,0,2*pi)

I already tried computing it by hand, looked in Bronstein, searched the internet, but didn't find any solution. But I'm no specialist in Analysis, so perhaps somebody can help? Clearly the series converges for every x in [0,2*pi] ...