how to fill region with color
HI
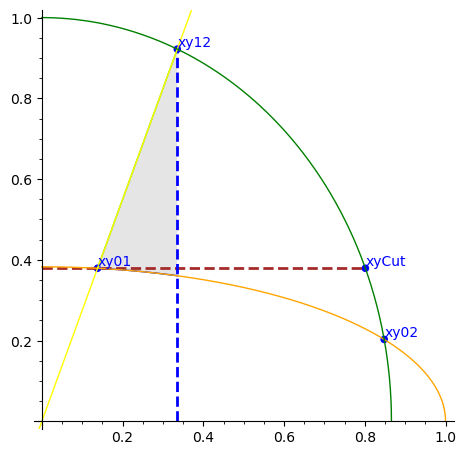
how to fill in gray only the region between the yellow curve the orange curve and the blue dashed line ?
var('x')
PtsL=[[0.13795, 0.37902], [0.33554, 0.92189], [0.84803, 0.2028], [0.80141, 0.37902]]
PtsNamesL=['xy01','xy12','xy02','xyCut']
ellipse0=1/2*sqrt(-x^2 + 1)*sqrt(-sqrt(2) + 2)
ellipse1=x*cos(1/9*pi)/sin(1/9*pi)
ellipse2=sqrt(-4/3*x^2 + 1)
plt=list_plot(PtsL,color='blue',size=30)
for i in range(len(PtsL)) :
plt+=text(PtsNamesL[i],vector(PtsL[i])*1.05, color='blue')
plt+=line([[0,PtsL[3][1]],PtsL[3]],color='brown',thickness=2,linestyle='dashed')
plt+=line([[PtsL[1][0],0],PtsL[1]],color='blue',thickness=2,linestyle='dashed')
plt+=plot([ellipse0, ellipse1,ellipse2], 0,1, fill={0: [1]}, fillcolor='#ccc')
plt+=plot(ellipse0,color='orange')
plt+=plot(ellipse1,color='yellow')
plt+=plot(ellipse2,color='green')
show(plt,xmin=0,xmax=1,ymin=0,ymax=1)