Positioning the nodes of a graph

edit

Say a graph G has nine vertices numbered 1 to 9 and we want the grid layout in the question.

One easily defines a dictionary of positions.

The set_pos method then lets us assign those positions to the graph.

The positions can also be set when creating the graph, using the pos=... optional argument.

For example, define the vertex set.

sage: V = [1 .. 9]

Then the position dictionary:

sage: pos = {v: (n % 3, -(n // 3)) for n, v in enumerate(V)}

Now build a graph with those vertices, no edges, and those positions:

sage: G = Graph([V, []], format='vertices_and_edges', pos=pos)

Plot it:

sage: G.plot()

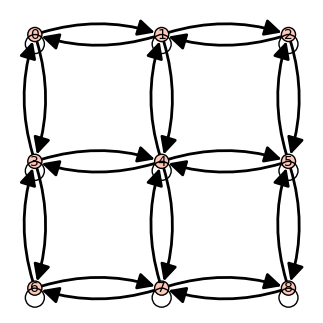
If we start from an adjacency matrix, the vertices will be numbered from 0.

Start from the matrix in the question and remove one of row (chosen so the resulting matrix is symmetric):

sage: A = matrix([[1, 1, 0, 1, 0, 0, 0, 0, 0],
....:         [1, 1, 1, 0, 1, 0, 0, 0, 0],
....:         [0, 1, 1, 0, 0, 1, 0, 0, 0],
....:         [1, 0, 0, 1, 1, 0, 1, 0, 0],
....:         [1, 0, 0, 1, 1, 0, 1, 1, 0],
....:         [0, 1, 0, 1, 1, 1, 0, 1, 0],
....:         [0, 0, 1, 0, 1, 1, 0, 0, 1],
....:         [0, 0, 0, 1, 0, 0, 1, 1, 0],
....:         [0, 0, 0, 0, 1, 0, 1, 1, 1],
....:         [0, 0, 0, 0, 0, 1, 0, 1, 1]])

sage: A.nrows(), A.ncols()
(10, 9)
sage: Arows = A.rows()
sage: del Arows[4]
sage: B = matrix(Arows)
sage: B.is_symmetric()
True

Define positions for vertices 0 to 8 and build a digraph from that matrix with those positions:

sage: pos = {n: (n % 3, -(n // 3)) for n in range(9)}
sage: D = DiGraph(B, format='adjacency_matrix', pos=pos)
sage: D.plot()

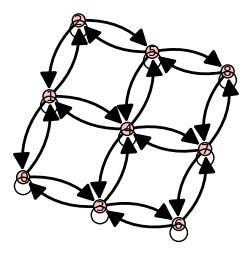
Note that without setting the positions ourselves, the default "spring" layout algorithm would already do a very good job on the grid graph, starting from the corrected matrix.

sage: D = DiGraph(B, format='adjacency_matrix)  # don't set pos
sage: D.plot()

The positions have not been set at the time of creating this graph. Defines pos as above, and running

sage: D.set_pos(pos)
sage: D.plot()

gives the same output as when we defined D = DiGraph(..., pos=pos) above.

Sage has a built-in GridGraph constructor which labels the vertices by their coordinates and positions them in a grid all by itself.

sage: G = graphs.GridGraph((3, 3))
sage: G.plot()

This gives an undirected graph.

Turning it into a directed graph is easy:

sage: D = DiGraph(G)

This preserves the positions!

One can also relabel the vertices:

sage: D.relabel([1 .. 9])

This also preserves the positions!

To sum up, the easiest way to achieve the graph in the question might be:

sage: D = DiGraph(graphs.GridGraph((3, 3)), loops=True)
sage: D.relabel([1 .. 9])
sage: D.add_edges((i, i) for i in D.vertices())
sage: D

Regarding the customisation of vertex and edges labels, start by checking the documentation and/or the many questions and answers on Ask Sage which provide instructive examples.