Tiny results of find root

edit

A few possible hints:

• without Sage: g(x) vanishes if, and only if, x^2 or cos(2*x) vanish, if, and only if, x=0 or there exists k in ZZ such that x = pi/4 + k*pi/2.

• now, plot the graph of g around zero:

  sage: g.plot()
  

• the root at zero is "double" (around zero, g is very similar to x^2), so that a small perturbation (due to numerical noise) of g could either lead to two (roughly opposite) zeros, or no zero at all.

• that said, 7.755077210568017e-09 is pretty huge for a numerical noise, how could that be ?

• note that 0.1 is not an exact floating-point number, as it can not be written with a finite binary expansion exactly, hence the addition of the step 0.1 with itself could lead to some accumulated shift, see the middle of the output of:

  sage: for num in [-10..10,step=.1]: 
  ....:     print(num)
  [...]
  -0.200000000000019
  -0.100000000000019
  -1.87905246917808e-14
  0.0999999999999812
  0.199999999999981
  0.299999999999981
  [...]
  

• compare

  sage: find_root(g,-0.100000000000019,-1.87905246917808e-14)                                                                                                                                                  
  -7.755114791616871e-09
  

  with

  sage: find_root(g,-0.1,0)                                                                                                                                                                                    
  0.0
  

Those two roots are both approximations of 0. If possible, you should always seek to solve theoretically and numerically. If the answers agree then you feel confident everything was done correctly. If the answers disagree then you have to look deeper. The roots of the function are when it is equal to 0, so you need to solve the equation (x^2)*cos(2*x)=0. That means either x=0 or cos(2*x)=0. Now cos(x)=0 at +/- (2k+1)pi/2 so cos(2x)=0 at +/- (2k+1)pi/4. Since we're looking for roots over [-10,10], this means our roots are 0, +/- pi/4, 3pi/4,....11pi/4. Your answer +/- 0.7853981633974483, 2.356194490192345, 3.9269908169872405, 5.497787143782152, 7.0685834705770345, 8.639379797371932 are the roots +/- pi/4, 3pi/4,....11pi/4. What's missing is 0. In your search for roots over [-.1,0] and [0,.1] you've found -7.755114791616843e-09 and 7.755114791616843e-09.

You mention inflection points but usually we calculate inflection points by taking the second derivative but from your answers I see you are setting the first derivative equal to 0. Where the derivative is 0 (or undefined) are usually called the critical values. If you rewrite the second answer as x=cot(2x) and think about the graphs of cot(2x) and x and where the intersect you'll get an idea of the number of answers. Try plotting

A = plot(cot(2*x),-10,10,ymax=10, ymin=-10, detect_poles=True)
B = plot(x,-10,10,ymax=10, ymin=-10,color='red')
(A+B).show()

Which looks like:

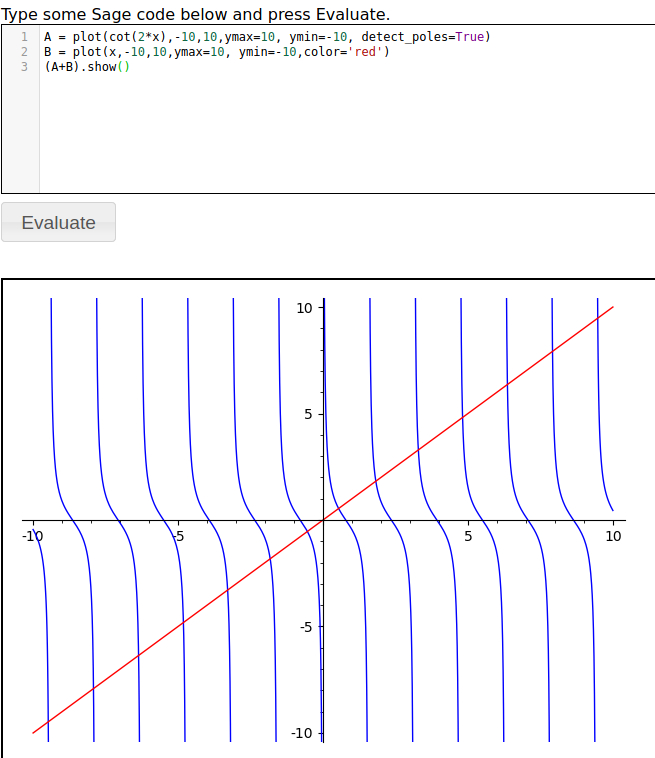
There is no way to solve that equation analytically. However, since you know where, approximately, the roots are you can use find_root , documentation here to find them. Your first positive solution would be found by, for example, find_root(cot(2*x)-x,.01,.8) to get 0.5384369931559019. What should become apparent is that learning mathematical theory can help you to use SAGE like an expert.