Why does plot choke on x to the 1/3 power, when it will calculate it just fine?

edit

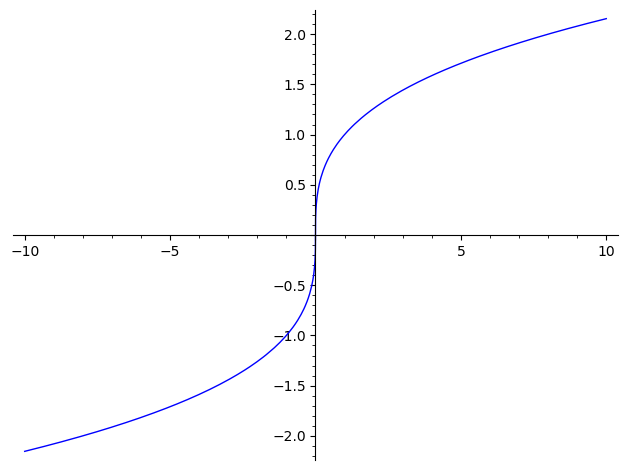
This question has been covered before, see here. Remember your order of operation: exponentiation doesn't apply to the negative. You've taken a positive cube root and then made it negative. If you try (-10)^(1/3).n() then you get 1.07721734501594 + 1.86579517236206*I.

Well, the plot comes out fine if I use sgn twice, but it's a bit obtuse, easy to mistype, and strikes me as a bit of a cheat. 😋 plot(sgn(x)*((sgn(x)*x)^(1/3)),-10,10)

And it bothers me that the cube root of -8 is -2, a real number. -2*-2*-2 = -8

Following the answers, both plot(sgn(x)*abs(x)^(1/3),(x,-10,10)), which uses sgn once and the more natural plot(lambda x: RR(x).nth_root(3), (-10, 10)) work. The RR is telling Sage that real roots are expected. See documentation here.

Thanks, I need to look into rings like RR, which I only vaguely understand.