Trigonometric equation solving

edit

This equation $e=0$ is polynomial in $c_1=\cos(t_1), s_1=\sin(t_1), c_2=\cos(t_2), s_2=\sin(t_2)$. Explicitly:

sage: var('t1,t2')
sage: eqn = (cos(t1)*cos(t2) - sin(t1)*sin(t2) - cos(t1))*(cos(t2)*sin(t1) + (cos(t1) + 1)*sin(t2)) - ((cos(t1) - 1)*cos(t2) - sin(t1)*sin(t2))*(cos(t2)*sin(t1) + cos(t1)*sin(t2) + sin(t1)) ==0
sage: R.<c1,s1,c2,s2> = PolynomialRing(QQ, order='lex')
sage: trig_to_poly = lambda expr: R(str(expr).replace('cos(t1)','c1').replace('sin(t1)','s1').replace('cos(t2)','c2').replace('sin(t2)','s2'))
sage: e = trig_to_poly(eqn.lhs()); e
-c1^2*s2 - 2*c1*s1*c2 + 2*c1*c2*s2 - c1*s2 + s1^2*s2 + s1*c2^2 + s1*c2 - s1*s2^2

Calculate a Groebner basis of the ideal $\langle e, c_1^2+s_1^2-1, c_2^2+s_2^2-1 \rangle$ in $\mathbb{Q}[c_1,s_1,c_2,s_2]$ with respect to the lexicographic monomial ordering $c_1 > s_1 > c_2 > s_2$:

sage: GB = R.ideal(e,c1^2+s1^2-1,c2^2+s2^2-1).groebner_basis(); GB
[c1^2 + s1^2 - 1, c1*s1 + 8*c1*s2^5 - 6*c1*s2^3 - 1/2*c1*s2 + 4*s1^3*c2 - 8*s1^3*s2^2 + 6*s1^3 - 16*s1^2*c2*s2^3 + 8*s1^2*c2*s2 - 8*s1^2*s2^3 + 6*s1^2*s2 + 8*s1*c2*s2^4 - 10*s1*c2*s2^2 + 1/2*s1*c2 + 8*s1*s2^4 - 4*s1*s2^2 - 3/2*s1 + 4*c2*s2^3 - c2*s2 + 8*s2^5 - 8*s2^3 + 3/2*s2, c1*c2*s2 - 8*c1*s2^5 + 8*c1*s2^3 - c1*s2 - 4*s1^3*c2 + 8*s1^3*s2^2 - 8*s1^3 + 16*s1^2*c2*s2^3 - 12*s1^2*c2*s2 + 8*s1^2*s2^3 - 6*s1^2*s2 - 8*s1*c2*s2^4 + 12*s1*c2*s2^2 - 2*s1*c2 - 8*s1*s2^4 + 5*s1*s2^2 + 2*s1 - 4*c2*s2^3 + 3*c2*s2 - 8*s2^5 + 10*s2^3 - 3*s2, c1*s2^7 - 5/4*c1*s2^5 + 5/16*c1*s2^3 + 1/2*s1^3*c2*s2^2 - 1/4*s1^3*c2 - s1^3*s2^4 + 5/4*s1^3*s2^2 - 1/4*s1^3 - 2*s1^2*c2*s2^5 + 2*s1^2*c2*s2^3 - 3/8*s1^2*c2*s2 - s1^2*s2^5 + 5/4*s1^2*s2^3 - 3/8*s1^2*s2 + s1*c2*s2^6 - 7/4*s1*c2*s2^4 + 11/16*s1*c2*s2^2 + s1*s2^6 - s1*s2^4 + 1/16*s1*s2^2 + 1/2*c2*s2^5 - 3/8*c2*s2^3 + s2^7 - 3/2*s2^5 + 9/16*s2^3, s1^4 + 2*s1^3*c2*s2 - s1^3*s2 - 2*s1^2*c2*s2^2 + 1/2*s1^2*c2 - 1/2*s1^2 - 3/2*s1*c2*s2 - s1*s2^3 + 3/2*s1*s2 + c2*s2^2 + s2^4 - s2^2, c2^2 + s2^2 - 1]

This system of equations is equivalent to the original one, but it is "more triangular". The (familiar) last equation GB[-1] depends only on $c_2, s_2$ (hence $t_2$). The second-to-last equation GB[-2] depends only on $s_1,c_2,s_2$; it is quartic in $s_1$ with leading coefficient $1$, so we can solve for $s_1$ in terms of $c_2,s_2$ (hence $t_2$). In fact:

sage: GB[-2].factor()
(1/2) * (-s1 + s2) * (-2*s1^3 - 4*s1^2*c2*s2 - s1*c2 + s1 + 2*c2*s2 + 2*s2^3 - 2*s2)

So either $s_1=s_2$ or $s_1$ is a (real) root of that cubic. The discriminant of the cubic is:

sage: D = GB[-2].factor()[1][0].discriminant(s1); D
512*c2^4*s2^4 + 16*c2^4*s2^2 + 512*c2^3*s2^6 - 512*c2^3*s2^4 - 320*c2^3*s2^2 - 8*c2^3 - 288*c2^2*s2^4 + 160*c2^2*s2^2 + 24*c2^2 - 576*c2*s2^4 + 576*c2*s2^2 - 24*c2 - 432*s2^6 + 864*s2^4 - 432*s2^2 + 8

On the circle $c_2^2+s_2^2=1$ it has only one zero, at $(1,0)$:

sage: S = PolynomialRing(QQ,names='c2,s2')
sage: S.ideal([c2^2+s2^2-1,D]).variety()
[{s2: 0, c2: 1}]

Even though it looks a bit like it has more:

sage: var('x,y,z,t')
sage: implicit_plot3d(z==0,(x,-1,1),(y,-1,1),(z,-1,1),color='yellow') + parametric_plot3d([cos(t),sin(t),D.subs({c2:cos(t),s2:sin(t)})], (t,0,2*pi)) + point3d((1,0,0))

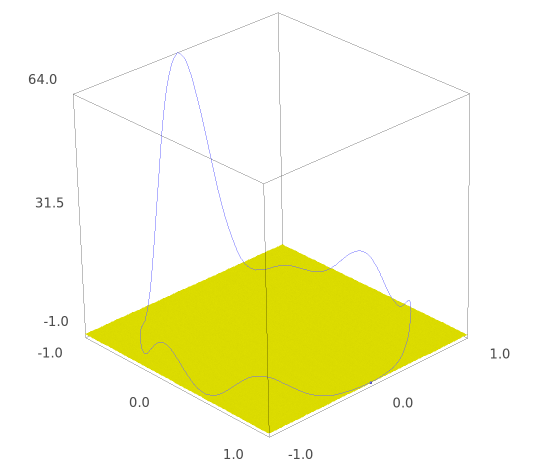
In any case, the discriminant of the cubic is $\geqslant 0$ on the circle $c_2^2+s_2^2=1$, so all roots of the cubic are real, and they are distinct when the discriminant is $\neq 0$; that is, away from $(1,0)$.

In conclusion: either $s_1 = s_2$ or $s_1$ is a real root of a cubic, which can be given by the cubic formula:

sage: SR(GB[-2]).solve(SR(s1))
[s1 == -2/3*c2*s2 - 1/36*(8*c2^2*s2^2 - 3*c2 + 3)*(-I*sqrt(3) + 1)/(-8/27*c2^3*s2^3 + 1/6*(c2 - 1)*c2*s2 + 1/2*s2^3 + 1/2*c2*s2 - 1/2*s2 + 1/6*sqrt(-1/3*(32*c2^3 - 27)*s2^6 - 2/3*(16*c2^4 - 16*c2^3 - 9*c2^2 - 18*c2 + 27)*s2^4 + 1/6*c2^3 - 1/3*(c2^4 - 20*c2^3 + 10*c2^2 + 36*c2 - 27)*s2^2 - 1/2*c2^2 + 1/2*c2 - 1/6))^(1/3) - 1/2*(-8/27*c2^3*s2^3 + 1/6*(c2 - 1)*c2*s2 + 1/2*s2^3 + 1/2*c2*s2 - 1/2*s2 + 1/6*sqrt(-1/3*(32*c2^3 - 27)*s2^6 - 2/3*(16*c2^4 - 16*c2^3 - 9*c2^2 - 18*c2 + 27)*s2^4 + 1/6*c2^3 - 1/3*(c2^4 - 20*c2^3 + 10*c2^2 + 36*c2 - 27)*s2^2 - 1/2*c2^2 + 1/2*c2 - 1/6))^(1/3)*(I*sqrt(3) + 1), s1 == -2/3*c2*s2 - 1/36*(8*c2^2*s2^2 - 3*c2 + 3)*(I*sqrt(3) + 1)/(-8/27*c2^3*s2^3 + 1/6*(c2 - 1)*c2*s2 + 1/2*s2^3 + 1/2*c2*s2 - 1/2*s2 + 1/6*sqrt(-1/3*(32*c2^3 - 27)*s2^6 - 2/3*(16*c2^4 - 16*c2^3 - 9*c2^2 - 18*c2 + 27)*s2^4 + 1/6*c2^3 - 1/3*(c2^4 - 20*c2^3 + 10*c2^2 + 36*c2 - 27)*s2^2 - 1/2*c2^2 + 1/2*c2 - 1/6))^(1/3) - 1/2*(-8/27*c2^3*s2^3 + 1/6*(c2 - 1)*c2*s2 + 1/2*s2^3 + 1/2*c2*s2 - 1/2*s2 + 1/6*sqrt(-1/3*(32*c2^3 - 27)*s2^6 - 2/3*(16*c2^4 - 16*c2^3 - 9*c2^2 - 18*c2 + 27)*s2^4 + 1/6*c2^3 - 1/3*(c2^4 - 20*c2^3 + 10*c2^2 + 36*c2 - 27)*s2^2 - 1/2*c2^2 + 1/2*c2 - 1/6))^(1/3)*(-I*sqrt(3) + 1), s1 == -2/3*c2*s2 + 1/18*(8*c2^2*s2^2 - 3*c2 + 3)/(-8/27*c2^3*s2^3 + 1/6*(c2 - 1)*c2*s2 + 1/2*s2^3 + 1/2*c2*s2 - 1/2*s2 + 1/6*sqrt(-1/3*(32*c2^3 - 27)*s2^6 - 2/3*(16*c2^4 - 16*c2^3 - 9*c2^2 - 18*c2 + 27)*s2^4 + 1/6*c2^3 - 1/3*(c2^4 - 20*c2^3 + 10*c2^2 + 36*c2 - 27)*s2^2 - 1/2*c2^2 + 1/2*c2 - 1/6))^(1/3) + (-8/27*c2^3*s2^3 + 1/6*(c2 - 1)*c2*s2 + 1/2*s2^3 + 1/2*c2*s2 - 1/2*s2 + 1/6*sqrt(-1/3*(32*c2^3 - 27)*s2^6 - 2/3*(16*c2^4 - 16*c2^3 - 9*c2^2 - 18*c2 + 27)*s2^4 + 1/6*c2^3 - 1/3*(c2^4 - 20*c2^3 + 10*c2^2 + 36*c2 - 27)*s2^2 - 1/2*c2^2 + 1/2*c2 - 1/6))^(1/3), s1 == s2]

Of course, $c_1 = \pm\sqrt{1-s_1}$. To obtain $t_1$, restrict the range and apply $\arccos$ or $\arcsin$.

In case $(c_2,s_2) = (1,0)$ you get:

sage: GB[-2].subs({c2:1,s2:0})
s1^4

so $s_1 = 0$ and hence $c_1 = \pm 1$.

Edit: It still needs to be checked/proved that the roots of the cubic have magnitude $\leq 1$.

Edit 2: The numerical solution by @ortollj suggests that the solutions are in fact very simple expressions. One could try to improve the above approach by adding extra variables for the sine and cosine of double and half the angles, and trigonometric identities such as double-angle and half-angle formulae.

It seems that the opening post is homework, since the equation can be solved by hand, if I am right. Anyway, let us see how.

Let $E$ be the left-hand side of the equation given in the opening post. It can be rewritten as follows: $$E= \begin{aligned}[t] & ( c_1c_2-s_1s_2-c_1)(s_1c_2+c_1s_2+s_2) \\ &-(c_1c_2-s_1s_2-c_2)(s_1c_2+c_1s_2+s_1), \end{aligned} $$ with $c_i=\cos(t_i)$, $s_i=\sin(t_i)$, for $i=1,2$. Since $$c_1c_2-s_1s_2 = \cos(t_1+t_2)$$ and $$s_1c_2+c_1s_2=\sin(t_1+t_2),$$ we get $$E= \begin{aligned}[t] & \Bigl( \cos(t_1+t_2)-\cos(t_1)\Bigr) \Bigl( \sin(t_1+t_2)+\sin(t_2)\Bigr) \\ &-\Bigl( \cos(t_1+t_2)-\cos(t_2)\Bigr) \Bigl( \sin(t_1+t_2)+\sin(t_1)\Bigr). \end{aligned} $$ Once again, using well know trigonometric formulae, we obtain $$E= \begin{aligned}[t] & \Bigl(-2\sin\frac{2t_1+t_2}{2}\sin\frac{t_2}{2}\Bigr) \Bigl(2\sin\frac{t_1+2t_2}{2}\cos\frac{t_1}{2}\Bigr) \\ &-\Bigl(-2\sin\frac{t_1+2t_2}{2}\sin\frac{t_1}{2}\Bigr) \Bigl(2\sin\frac{2t_1+t_2}{2}\cos\frac{t_2}{2}\Bigr). \end{aligned} $$ Hence $$E= 4 \sin\frac{2t_1+t_2}{2} \sin\frac{t_1+2t_2}{2} \Bigl(\sin\frac{t_1}{2}\cos\frac{t_2}{2} -\cos\frac{t_1}{2}\sin\frac{t_2}{2}\Bigr),$$ that is, $$E= 4 \sin\frac{2t_1+t_2}{2}\ \sin\frac{t_1+2t_2}{2} \ \sin\frac{t_1-t_2}{2}.$$ Therefore, $E=0$ if and only if, for some $k\in\mathbb{Z}$, $2t_1+t_2=2k\pi$ or $t_1+2t_2=2k\pi$ or $t_1-t_2=2k\pi$. It is now quite obvious how to get $t_1$ in terms of $t_2$.