Plot all complex numbers, for which a predicate holds
How do I solve the following exercise in SageMath?
Outline (in the complex number plane) all numbers z in ℂ, for which abs(z+2)^2 > abs(z-2*I)^2+1 holds.
So, I figured the first step is to actually solve the inequation:
sage: sol=solve(abs(z+2)^2 > abs(z-2*I)^2+1, z) #0: solve_rat_ineq(ineq=(_SAGE_VAR_z+2)^2 > abs(_SAGE_VAR_z-2*%i)^2+1)
sage: sol
[[z < (2*I), (4*I + 4)*z + 7 > 0],
[z == (2*I), (8*I - 1) > 0],
[(2*I) < z, (4*I + 4)*z + 7 > 0]]Okay, first, how do I interpret this solution? Every element in the list is a list of terms that must all hold? And of course, how can I now plot all those solutions?

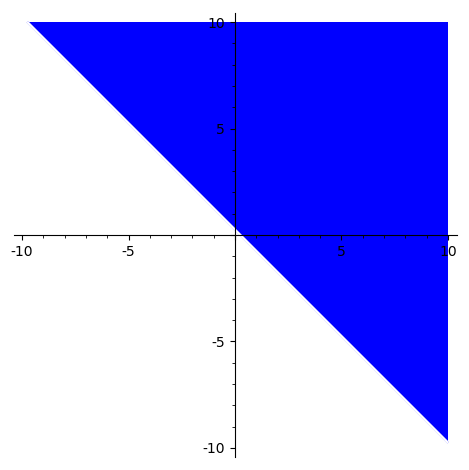

It seems that teaching SageMath to do |x+iy|2=x2+y2 is harder than doing it by hand.