How to draw the following graph
I want to write the following code in sagemath but unable to write it:
Suppose we consider the group $\Bbb Z_n$.
We consider an element $a\in \Bbb Z_n$ and form the subgroup generated by $a$ i.e. $\langle a\rangle ={a,2a,3a,\ldots 0}.$
We form a graph $G$ whose vertices are $\langle a\rangle $ and $\langle a\rangle $ and $\langle b\rangle $ are adjacent if either $\langle a\rangle \subset \langle b\rangle $ or $\langle b\rangle \subset \langle a\rangle $ .
How to plot the graph $G$ is Sagemath?
I am giving an example to clear the question:
Consider $\Bbb Z_4$ then consider $\langle 0\rangle $, $ \langle 1\rangle$ , $ \langle 2\rangle$, $ \langle 3\rangle$
Clearly $\langle 0\rangle ={0}$, $ \langle 1\rangle={1,2,3,0}$ , $ \langle 2={2,0}\rangle$, $ \langle 3={0,1,2,3}\rangle$.
Thus the graph $G$ has vertices as $\langle 0\rangle $, $ \langle 1\rangle$ , $ \langle 2\rangle$, $ \langle 3\rangle$ and $\langle 0\rangle $ is adjacent to $ \langle 1\rangle$ , $ \langle 2\rangle$, $ \langle 3\rangle$,
$\langle 1\rangle $ is adjacent to $ \langle 2\rangle$ , $ \langle 0\rangle$,
$\langle 2\rangle $ is adjacent to $ \langle 1\rangle$ , $ \langle 0\rangle$, $ \langle 3\rangle$
and $\langle 3\rangle $ is adjacent to $ \langle 0\rangle$, $ \langle 2\rangle$
Thus $G$ becomes

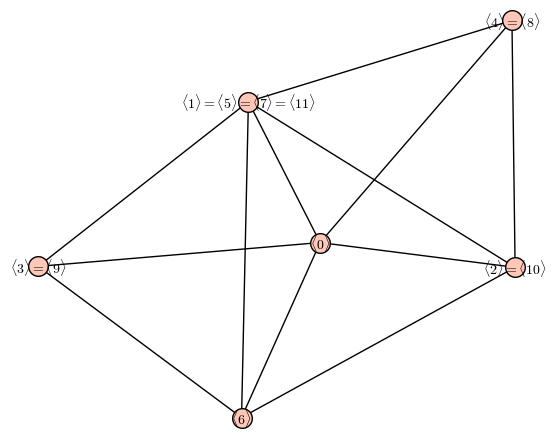

Why are $1$ and $3$ different vertices in your graph? They generate the same additive subgroup, i.e. $\langle 1\rangle = \langle 3 \rangle$.
Regarding the picture, i would say that @Captcha means that the vertices are elements of $\mathbb{Z}_n$, not its subgroups