1

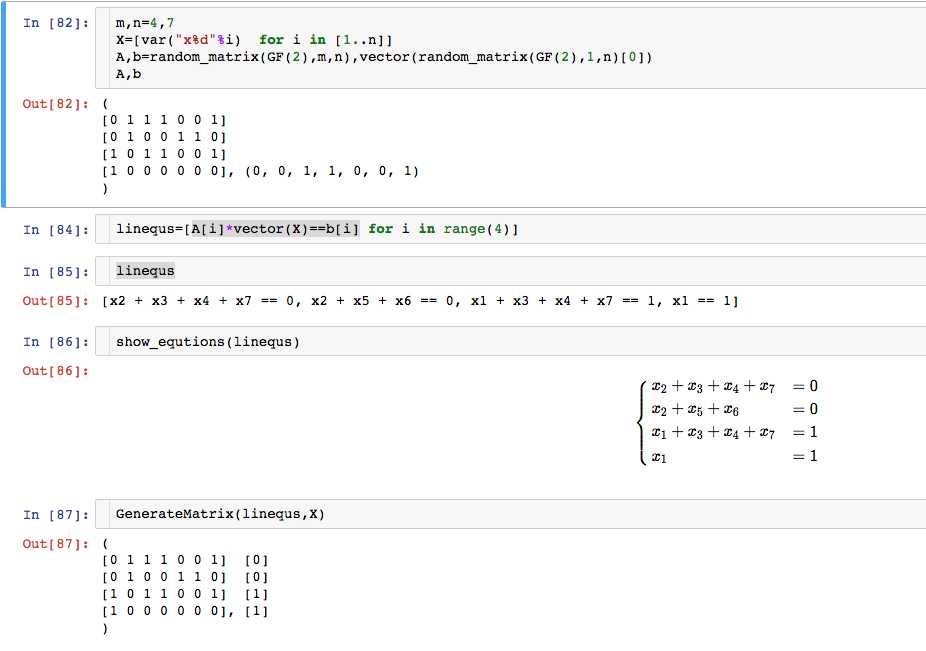
Turning system of linear equations into a matrix

linearalgebra

asked 2017-03-23 18:04:12 +0100

Anonymous

I have a very long list of equations (10^3 order of magnitude), but all linear. There are around 10^2 variables.

I would like to solve these equations in $F_2$, that is, in the field of 2 elements. Questions:

Is there a handy-dandy "solve" command in Sage that allows me to list these equations, specify the field in which I want these equations to be interpreted, and Sage returns an answer?
Or, is there a handy-dandy way I can input a list of linear equations, and Sage automatically returns a matrix? So long as I can read off which entries/columns of the matrix correspond to which variables in my original equations, I'm happy to then use commands taking matrices as inputs, and use the answer to the question "Solve large system of linear equations over GF(2)" (I would put the link in, but I don't have the karma).

edit retag flag offensive close merge delete

1 Answer

Sort by » oldest newest most voted

1

answered 2017-03-24 15:10:53 +0100

danny
173 ●3 ●9 ●20

I give an answer for question 2. See the following : image description

The definition of GenerateMatrix is:

def GenerateMatrix(equsys, vars):
A=matrix([[equ.lhs().coefficient(v) for v in vars] for equ in equsys])
b=matrix([[equ.rhs()] for equ in equsys])
return (A,b)

edit flag offensive delete link

Comments

What is show_equtions?

slelievre ( 2018-07-18 12:01:30 +0100 )edit

Your Answer

Please start posting anonymously - your entry will be published after you log in or create a new account.

Question Tools

1 follower

Stats

Asked: 2017-03-23 18:03:46 +0100

Seen: 1,399 times

Last updated: Mar 24 '17

Related questions

Copyright Sage, 2010. Some rights reserved under creative commons license. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.

Powered by Askbot version 0.7.59