<?xml version="1.0" encoding="utf-8"?>
<rss xmlns:atom="http://www.w3.org/2005/Atom" version="2.0"><channel><title>ASKSAGE: Sage Q&A Forum - RSS feed</title><link>https://ask.sagemath.org/questions/</link><description>Q&A Forum for Sage</description><atom:link href="https://ask.sagemath.org/feeds/rss/" rel="self"></atom:link><language>en</language><copyright>Copyright Sage, 2010. Some rights reserved under creative commons license.</copyright><lastBuildDate>Mon, 29 May 2023 02:38:11 +0200</lastBuildDate><item><title>How can I correct this error?</title><link>https://ask.sagemath.org/question/68828/how-can-i-correct-this-error/</link><description> %display latex
l=2
m=3
M = Manifold(4, 'M', structure='Lorentzian')
X.<t,r,th,ph> = M.chart('t r th ph')
U=(2*m*t+l^2-t^2)/(t^2+l^2)
g = M.metric()
g[0,0] = -1/U
g[1,1] = 4*l^2*U
g[1,3] = 4*l^2*U*cos(th)
g[2,2] = t^2+l^2
g[3,3] = 4*l^2*U*(cos(th))^2+(t^2+l^2)*(sin(th))^2
g.display()
R3 = Manifold(3, 'R^3', latex_name=r'\mathbb{R}^3')
X3.<x,y,z> = R3.chart()
to_R3 = M.diff_map(R3, {(X, X3): [r*sin(th)*cos(ph),
r*sin(th)*sin(ph), r*cos(th)]})
to_R3.display()
p0 = M.point((7, 30, 0, 0), name='p_0')
v0 = M.tangent_space(p0)((1, 53/12, 0, 0), name='v_0')
v0.display()
s = var('s')
geod = M.integrated_geodesic(g, (s, 0, 10), v0); geod
sol = geod.solve()
interp = geod.interpolate()
graph = geod.plot_integrated(chart=X3, mapping=to_R3, label_axes=True, plot_points=10)
graph += p0.plot(chart=X3, mapping=to_R3)
graph += sphere(color='grey')
show(graph)
lsoda-- at t (=r1), too much accuracy requested
for precision of machine.. see tolsf (=r2)
in above, r1 = 0.1000000000000D+00 r2 = NaN
/home/sc_serv/sage/local/var/lib/sage/venv-python3.10/lib/python3.10/site-packages/scipy/integrate/_odepack_py.py:247: ODEintWarning: Excess accuracy requested (tolerances too small). Run with full_output = 1 to get quantitative information.
warnings.warn(warning_msg, ODEintWarning)
lsoda-- at t (=r1), too much accuracy requested
for precision of machine.. see tolsf (=r2)
in above, r1 = 0.1000000000000D+00 r2 = </description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Jack Zuffante</dc:creator><pubDate>Mon, 29 May 2023 02:38:11 +0200</pubDate><guid>https://ask.sagemath.org/question/68828/</guid></item><item><title>set precision for pari in Sage</title><link>https://ask.sagemath.org/question/61582/set-precision-for-pari-in-sage/</link><description> In the pari program, we can use \pb 256 to set the precision. For the pari in Sage, how to use this command ?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Lee</dc:creator><pubDate>Wed, 23 Mar 2022 08:37:44 +0100</pubDate><guid>https://ask.sagemath.org/question/61582/</guid></item><item><title>Precision in bits</title><link>https://ask.sagemath.org/question/60611/precision-in-bits/</link><description>how do you convert precision in bits to number of decimal digits ? I couldn't find out the formula. googling didn't help either. What I'm asking is;
print(N(pi, prec=2)) gives 3.0
print(N(pi, prec=4)) gives 3.2
print(N(pi, prec=6)) gives 3.1
print(N(pi, prec=12)) gives 3.14
etc.
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">user257</dc:creator><pubDate>Mon, 10 Jan 2022 19:58:19 +0100</pubDate><guid>https://ask.sagemath.org/question/60611/</guid></item><item><title>Precision in bits</title><link>https://ask.sagemath.org/question/60610/precision-in-bits/</link><description> how do you convert precision in bits to number of decimal digits ? I couldn't find out the formula. googling didn't help either
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">user257</dc:creator><pubDate>Mon, 10 Jan 2022 19:50:17 +0100</pubDate><guid>https://ask.sagemath.org/question/60610/</guid></item><item><title>Set Precision or Decimal places in symbolic expression</title><link>https://ask.sagemath.org/question/57300/set-precision-or-decimal-places-in-symbolic-expression/</link><description> Hello. I am currently working with some cumbersome symbolic expressions containing lots of variables. The issue I have is that I cannot view my symbolic expressions with as few decimal places as I would like. Here is a simplified example:
sage: var('x','y','z')
(x, y, z)
sage: expr = 0.1*x+0.2*y+0.3333*z
sage: show(expr)
0.100000000000000*x + 0.200000000000000*y + 0.333300000000000*z
Ideally I would like sth like:
sage: show(expr(precision=1))
0.1*x + 0.2*y + 0.3*z
or
sage: show(expr(decimals=2))
0.10*x + 0.20*y + 0.33*z</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">yorgos_sot</dc:creator><pubDate>Thu, 27 May 2021 16:34:00 +0200</pubDate><guid>https://ask.sagemath.org/question/57300/</guid></item><item><title>How to format the output of integrate() function when printing?</title><link>https://ask.sagemath.org/question/57036/how-to-format-the-output-of-integrate-function-when-printing/</link><description> I want to compute the integral of a function like this:
fi = -0.000004*x^4*y^3+0.000015*x^4*y^2
print(integrate(fi,x))
It prints:
-(8e-07)*x^5*y^3 + (3e-06)*x^5*y^2
Is there a way to format the output so that:
- it uses normal decimal notation instead of exponential one (-0.0000008 instead of -(8e-07))
- it has a given precision (it will print 0.000001 instead of 0.000001111 for example)
I know how to do this with a single variable but not when displaying what the integrate() function returns.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">MichaelTheSlav</dc:creator><pubDate>Sun, 09 May 2021 16:46:15 +0200</pubDate><guid>https://ask.sagemath.org/question/57036/</guid></item><item><title>canonicalize_radical() and evaluation return different answers</title><link>https://ask.sagemath.org/question/54084/canonicalize_radical-and-evaluation-return-different-answers/</link><description>This code return proof that f^8(x)=f(f(f(f(f(f(f(f(x))))))))=x if f(x)=(x(sqrt(2)-1)-1)/(x-1):
def yx(x):
cst=sqrt(2)-1
if(x==1):
return -Infinity
return (cst*x-1)/(x-1)
tmp=x
for t in range(1,9):
tmp=(yx(tmp)).canonicalize_radical()
print(t, tmp.canonicalize_radical())
But this code looks directly at orbit of a point and shows that the statement above is false:
tmp=1.5
lst=[]
for t in range(1,9):
tmp=(yx(tmp)).canonicalize_radical()
print(t, tmp.canonicalize_radical().n(80))
lst.append((t,tmp.n()))
By giving the next output:
1 -0.75735931288071485359493
2 0.74754689570642838213503
3 2.7345908033901357840028
4 0.076504843704676803069591
5 1.0485281374238889523706
6 0.13254046199725214558851
7 -0.090964954340477885594991
8 0.35391568118499587774957
Why the output is so different? Bit precision don't seem to be a problem.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Alex Karenin</dc:creator><pubDate>Fri, 30 Oct 2020 00:10:19 +0100</pubDate><guid>https://ask.sagemath.org/question/54084/</guid></item><item><title>Incorrect results for comparison expression</title><link>https://ask.sagemath.org/question/53548/incorrect-results-for-comparison-expression/</link><description>Sage incorrectly evaluates `bool(1/47749 <= -5564456128*e + 15125759978)` as False.
In more detail, consider this:
sage: x = -5564456128*e + 15125759978
sage: (1/47749).n(digits=6)
0.0000209428
sage: x.n(digits=20)
0.000020943072740919888020
sage: bool(1/47749 <= x)
False
What is going on? Why does the last boolean evaluate to False? This results in the failure of the assertion that `1/ceil(1/x) <= x`, which should be true mathematically.
Is there a way to compare two quantities that will result in a correct answer, using as much precision as necessary?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">svat</dc:creator><pubDate>Wed, 23 Sep 2020 09:48:15 +0200</pubDate><guid>https://ask.sagemath.org/question/53548/</guid></item><item><title>How to make Taylor expansion with fixed numerical precision?</title><link>https://ask.sagemath.org/question/49175/how-to-make-taylor-expansion-with-fixed-numerical-precision/</link><description>Following command
f(x)=sin(x)
taylor(f,x,1.0,2)
shows result:
x |--> -0.4207354924039483*(x - 1.0)^2 + 0.5403023058681398*x + 0.30116867893975674
The precision of result has too many bits, what I want is 3 bits, such as:
x |--> -0.420*(x - 1.0)^2 + 0.540*x + 0.301
How to do it?
Thanks for your help.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">John Bao</dc:creator><pubDate>Wed, 25 Dec 2019 05:37:23 +0100</pubDate><guid>https://ask.sagemath.org/question/49175/</guid></item><item><title>Set global RealNumber precision in .sage file</title><link>https://ask.sagemath.org/question/48094/set-global-realnumber-precision-in-sage-file/</link><description>I want to change the real number precision from 53 to, say, 100.
I found this very similar question: ask.sagemath.org/question/7887/set-global-precision-for-reals/ (sorry it doesn't let me post a link), which says to use
`R=RealField(100); RealNumber=R`
I tried it and it only works for me in the sage commandline, but not in .sage programs. Why is that and how do I get around it?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ytum</dc:creator><pubDate>Sun, 29 Sep 2019 13:03:05 +0200</pubDate><guid>https://ask.sagemath.org/question/48094/</guid></item><item><title>How to print the numeric part of a symbolic expression with arbitrary precision?</title><link>https://ask.sagemath.org/question/46468/how-to-print-the-numeric-part-of-a-symbolic-expression-with-arbitrary-precision/</link><description>How to print the numeric part of a symbolic expression with arbitrary precision?
I have a matrix `Hf`, it is a 3 by 3 matrix. It's a symbolic matrix, with just one variable 'E'. But on printing it, I get the as shown below. Basically what I want is to approximate the numerical part of the expression to arbitrary precision (let's say 3 decimal points), so that I can get a much cleaner expression.
sage: Hf.str()
[(𝟼.𝟶𝟿𝟶𝟻𝟸𝟼𝟺𝟼𝟻𝟿𝟺𝟺𝟿𝟽𝚎⎯𝟼)*(𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒))/𝙴⎯𝟶.𝟶𝟶𝟶𝟸𝟷𝟽𝟼𝟷𝟹𝟾𝟸𝟻𝟷𝟶𝟶𝟶𝟶𝟼*(𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)⎯𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒))/𝙴+𝟷𝟶𝟶𝟶⎯𝟶.𝟶𝟶𝟶𝟸𝟷𝟽𝟼𝟷𝟹𝟾𝟸𝟻𝟷𝟶𝟶𝟶𝟶𝟼*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))/𝙴+(𝟼.𝟶𝟿𝟶𝟻𝟸𝟼𝟺𝟼𝟻𝟿𝟺𝟺𝟿𝟽𝚎⎯𝟼)*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)⎯𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))/𝙴𝟶.𝟶𝟶𝟶𝟸𝟷𝟷𝟻𝟸𝟹𝟸𝟿𝟾𝟼𝟹𝟺𝟶𝟼𝟷*𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)/𝙴][⎯𝟶.𝟶𝟶𝟶𝟷𝟻𝟼𝟸𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶*𝚜𝚚𝚛𝚝(𝟸)*(𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)⎯𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒))*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)/𝙴+(𝟺.𝟼𝟾𝟽𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝚎⎯𝟼)*(𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒))*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)⎯𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))/𝙴⎯𝟶.𝟶𝟶𝟶𝟷𝟻𝟼𝟸𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶*𝚜𝚚𝚛𝚝(𝟸)*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)/𝙴+(𝟺.𝟼𝟾𝟽𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝚎⎯𝟼)*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)⎯𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))ˆ𝟸/𝙴⎯(𝟺.𝟼𝟾𝟽𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝚎⎯𝟼)*𝚜𝚚𝚛𝚝(𝟸)*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)⎯𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)/𝙴+𝟶.𝟶𝟶𝟶𝟹𝟷𝟸𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)ˆ𝟸/𝙴][⎯𝟶.𝟶𝟶𝟶𝟷𝟻𝟼𝟸𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶*𝚜𝚚𝚛𝚝(𝟸)*(𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)⎯𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒))*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)/𝙴+(𝟺.𝟼𝟾𝟽𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝚎⎯𝟼)*(𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒))*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))/𝙴⎯𝟶.𝟶𝟶𝟶𝟷𝟻𝟼𝟸𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶*𝚜𝚚𝚛𝚝(𝟸)*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)/𝙴+(𝟺.𝟼𝟾𝟽𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝚎⎯𝟼)*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)⎯𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))/𝙴⎯(𝟺.𝟼𝟾𝟽𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝚎⎯𝟼)*𝚜𝚚𝚛𝚝(𝟸)*(𝚜𝚚𝚛𝚝(𝟸)*𝚜𝚒𝚗(𝟽/𝟹𝟼*𝚙𝚒)*𝚜𝚒𝚗(𝟷/𝟷𝟾*𝚙𝚒)+𝚜𝚚𝚛𝚝(𝟸)*𝚌𝚘𝚜(𝟽/𝟹𝟼*𝚙𝚒))*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)/𝙴+𝟶.𝟶𝟶𝟶𝟹𝟷𝟸𝟻𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶𝟶*𝚌𝚘𝚜(𝟷/𝟷𝟾*𝚙𝚒)ˆ𝟸/𝙴]</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">jonespanicker</dc:creator><pubDate>Mon, 06 May 2019 22:18:37 +0200</pubDate><guid>https://ask.sagemath.org/question/46468/</guid></item><item><title>Homomorphisms lifted from base ring in PowerSeriesRing do not preserve precision</title><link>https://ask.sagemath.org/question/45002/homomorphisms-lifted-from-base-ring-in-powerseriesring-do-not-preserve-precision/</link><description>Hi all,
Homomorphisms which are lifted from the base ring seem to be unaware that precision exists in power/Laurent series rings. For example:
sage: R.<x> = PowerSeriesRing(ZZ)
sage: f = Hom(ZZ, ZZ)([1])
sage: Rf = Hom(R, R)(f); Rf
Ring endomorphism of Power Series Ring in x over Integer Ring
Defn: Induced from base ring by
Ring endomorphism of Integer Ring
Defn: 1 |--> 1
sage: Rf(1 + x + O(x^2))
1 + x
Can someone confirm that the expected output should be 1 + x + O(x^2), and that this is a bug?
Thanks,
Henry</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">liu.henry.hl</dc:creator><pubDate>Fri, 11 Jan 2019 02:06:35 +0100</pubDate><guid>https://ask.sagemath.org/question/45002/</guid></item><item><title>a.N(3) DID WORK past now only N(a,3) ???</title><link>https://ask.sagemath.org/question/44914/an3-did-work-past-now-only-na3/</link><description>
so, I updated from 6.1 to 8.5 due 6.1 did not complied!
Old sheets dose not work due I used notation a.N(3)
and it's equalent N(a,3) works still ???
Where is the cat ?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">joniboy</dc:creator><pubDate>Sun, 06 Jan 2019 17:20:46 +0100</pubDate><guid>https://ask.sagemath.org/question/44914/</guid></item><item><title>Incorrect result for comparison (precision issues?)</title><link>https://ask.sagemath.org/question/32371/incorrect-result-for-comparison-precision-issues/</link><description> Consider this session:
sage: if log(10) * 248510777753 < log(1024) * 82553493450:
....: print 'Less'
....: else:
....: print 'Not less'
....:
Not less
or more simply:
sage: bool(log(10)*248510777753 < log(1024)*82553493450)
False
But this is wrong, as we can see with higher-precision arithmetic:
sage: import mpmath
sage: mpmath.mp.dps = 22 # or anything greater
sage: bool(mpmath.log(10)*248510777753 < mpmath.log(1024)*82553493450)
True
I guess this is happening because Sage is computing to some finite precision. But when writing some bigger program, it's scary that a condition involving variables, like say,
if m * q < n * p:
can without warning give the wrong result and take the wrong path. Is there a way to prevent this from happening, i.e. to make sure that in the program, comparisons are done using as many bits of precision as are necessary to evaluate them correctly, without us having to pre-specify a precision (which may be both too large and wasteful, or too small and give incorrect results)?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ShreevatsaR</dc:creator><pubDate>Fri, 29 Jan 2016 04:58:13 +0100</pubDate><guid>https://ask.sagemath.org/question/32371/</guid></item><item><title>Precision plots - How do I do those?</title><link>https://ask.sagemath.org/question/29231/precision-plots-how-do-i-do-those/</link><description>Hi.
I have a function which varies so slowly, that in the range I'm interested only the 17th decimal changes.
The sws is this:
sage: mp = 139570180.
sage: mm = 105658371.5
sage: mn = 1.
sage: dmp = 350.
sage: dmm = 3.8
sage: dmn = 0.1
sage: l(a,b,c) = a^2 + b^2 + c^2 - 2*( a*b + b*c + c*a )
sage: f(x) = sqrt(l(mp^2, mm^2, x^2))/(2*mp)
sage: R=RealField(100)
sage: g = fast_callable(f, vars=[x], domain=R)
sage: plot( g, (x,0,2))
but I got the following plot, which is unsatisfactory in several ways!
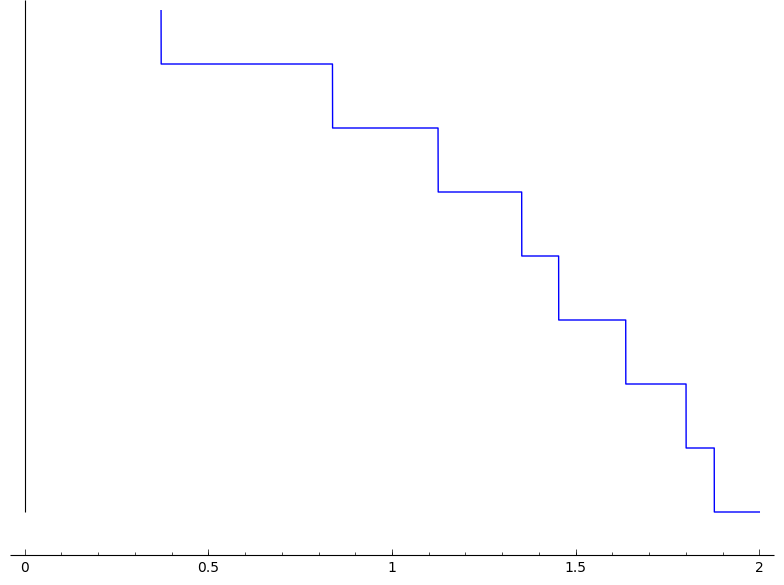
How could I possible improve it? (ticks on vertical axis, a "continuous" line, ...)
Thank you!</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Dox</dc:creator><pubDate>Thu, 20 Aug 2015 21:17:53 +0200</pubDate><guid>https://ask.sagemath.org/question/29231/</guid></item><item><title>Set the precision of imported methods</title><link>https://ask.sagemath.org/question/10760/set-the-precision-of-imported-methods/</link><description>How to set the precision of "numpy" methods?
e.g., for calculating the singular values of a matrix using numpy methods
sage: R = RealField(100)
sage: R
Real Field with 100 bits of precision
sage: A = matrix(R ,2,2, [1.746, 0.940, 1.246, 1.898])
sage: A
[ 1.7460000000000000000000000000 0.94000000000000000000000000000]
[ 1.2460000000000000000000000000 1.8980000000000000000000000000]
sage: A.parent()
Full MatrixSpace of 2 by 2 dense matrices over Real Field
with 100 bits of precision
sage: A = np.array(A) # the precision (100 bits) does not preserve in "numpy"
sage: U,sig,V = numpy.linalg.svd(A)
sage: sig
array([ 1.08490731e+06, 1.97535694e+00])
# the precision (100 bits) does not preserve in "numpy", hey only 8 digits here
----------
[NumPy Data types](http://docs.scipy.org/doc/numpy/user/basics.types.html)
> sage: np.array([1, 2, 3], dtype='f')
> array([ 1., 2., 3.], dtype=float32)
That's a choice. However, I'd like some more convenient method like "numpy.set_digits(100)"...
----------
Thanks in advance!
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">gundamlh</dc:creator><pubDate>Thu, 21 Nov 2013 11:01:49 +0100</pubDate><guid>https://ask.sagemath.org/question/10760/</guid></item><item><title>precision when using numpy</title><link>https://ask.sagemath.org/question/10542/precision-when-using-numpy/</link><description>when using numpy, do i have to take care of the ranges for integers, floats, ..etc. and what if the number exceeds the limits for int64 or float64, what shall i do then ? and does this problem exist als for the normal integer data type in sage ('sage.rings.integer.Integer'> ) ???</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Mohamed Gaafar</dc:creator><pubDate>Fri, 25 Oct 2013 15:37:07 +0200</pubDate><guid>https://ask.sagemath.org/question/10542/</guid></item><item><title>computing the digist of Pi</title><link>https://ask.sagemath.org/question/10274/computing-the-digist-of-pi/</link><description>I tried to code the Salamin-Brent iteration. I calculated with exact numbers and the procedure returned the numerical value with the .n() function. The iteration was very very slow, for 20 iterations it is approximately 900 secs. (In Maple the same code is 0.06 secs). Can I modify the numerical precision in every step with some method? (Because in every step the number of correct digits is doubling )</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">czsan</dc:creator><pubDate>Tue, 25 Jun 2013 06:24:38 +0200</pubDate><guid>https://ask.sagemath.org/question/10274/</guid></item><item><title>Accuracy versus precision of algebraic number calculations</title><link>https://ask.sagemath.org/question/10054/accuracy-versus-precision-of-algebraic-number-calculations/</link><description>Hi everyone - another very basic question from me ...
I am doing some calculations of absolute norms of determinants of matrices whose entries come from cyclotomic fields. The (rational) numbers which are output are sensible but occasionally have massive prime numbers as factors which I was not expecting. My question is whether I can rely upon such numbers when they are output by SAGE's calculations inside a specified number field, or whether somewhere along the way some imprecision may have been introduced which results in a "distorted" prime number being a factor of the output.
Another stylized way of asking the same thing: is it possible that the answer to some question involving a small prime p might actually contain a factor of p^100, but nevertheless because of accumulated rounding errors etc I have ended up with p^100-2 which happens to be prime? Or does SAGE "know" only to output perfect answers involving algebraic number fields, even when the heights involved are that big?
Many thanks</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">GaryMak</dc:creator><pubDate>Tue, 23 Apr 2013 07:27:41 +0200</pubDate><guid>https://ask.sagemath.org/question/10054/</guid></item><item><title>rounding error .n() and N()</title><link>https://ask.sagemath.org/question/9282/rounding-error-n-and-n/</link><description>Why does 1.414 - sqrt(2).n(digits=4) not evaluate to zero?
sage: sqrt(2).n(digits=4)
1.414
sage: 1.414 - sqrt(2).n(digits=4)
-0.0002136
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">kjhudson</dc:creator><pubDate>Mon, 08 Apr 2013 11:53:32 +0200</pubDate><guid>https://ask.sagemath.org/question/9282/</guid></item><item><title>Arbitrary precision with power function</title><link>https://ask.sagemath.org/question/9788/arbitrary-precision-with-power-function/</link><description>Hello! Sorry for my english.
Why in Sage 5.6
> numerical_approx((3**2.72), digits=200)
gives
> 19.850425152727527944307439611293375492095947265625000000000000000000000\
000000000000000000000000000000000000000000000000000000000000000000000000\
000000000000000000000000000000000000000000000000000000000
and
> RealField(1000)(3**2.72)
gives
> 19.850425152727527944307439611293375492095947265625000000000000000000000\
000000000000000000000000000000000000000000000000000000000000000000000000\
000000000000000000000000000000000000000000000000000000000000000000000000\
000000000000000000000000000000000000000000000000000000000000000000000000\
0000000000000
? After digit 5 zero, zero, zero. How to get more digits in Sage?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">PlezzeR</dc:creator><pubDate>Fri, 08 Feb 2013 21:53:21 +0100</pubDate><guid>https://ask.sagemath.org/question/9788/</guid></item><item><title>Precision of find_root</title><link>https://ask.sagemath.org/question/9328/precision-of-find_root/</link><description>Here is a straightforward question:
I am wondering about the precision of find_root. Looking into the documentation (I'm using Sage v. 5.0), there is a comment along with one of the examples that the "precision isn't very good on some machines." At the same time, it says that the routine converges unless it throws an error.
A post [response](http://www.mail-archive.com/sage-support@googlegroups.com/msg16187.html) from William Stein clarifies that the function is passed to SciPy which has double precision. So I'm assuming that there may be a way for more precision on some machines, but that one can always count on having at least this much.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">TumericTJ</dc:creator><pubDate>Mon, 17 Sep 2012 22:28:51 +0200</pubDate><guid>https://ask.sagemath.org/question/9328/</guid></item><item><title>adding real literal and real number of high precision</title><link>https://ask.sagemath.org/question/9185/adding-real-literal-and-real-number-of-high-precision/</link><description>When Sage is adding a real literal to a real number of high precision, shouldn't it calculate the sum in the high precision ring? Instead, Sage seems to calculate in double precision:
RF=RealField(150); RF
Real Field with 150 bits of precision
RF(0.9 + RF(1e-18))
0.90000000000000002220446049250313080847263336
RF(1.0+ RF(1e-18))
1.0000000000000000000000000000000000000000000
RF(1+ RF(1e-18))
1.0000000000000000010000000000000000000000000
I'm trying to use high precision arithmetic (2658 bits) in Sage to verify some results produced by the high precision semidefinite program solver sdpa_gmp. Sage's treatment of real literals in these calculations has made me anxious about the possibility that I'm overlooking other ways in which the calculations might be unreliable.
Is there anywhere an explanation of Sage's treatment of real literals in high precision arithmetic?
Added:
Immediately after posting this question, the list of Related Questions in the sidebar pointed me to question/327/set-global-precision-for-reals where I learned that 'RealNumber = RF' would make all real literals lie in the high precision ring. Still, I wonder why the default behavior is to discard precision that is present in the original real literal.
thanks,
Daniel Friedan
thanks for </description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Daniel Friedan</dc:creator><pubDate>Fri, 27 Jul 2012 13:05:52 +0200</pubDate><guid>https://ask.sagemath.org/question/9185/</guid></item><item><title>Why is 3e1 not equivalent to 30?</title><link>https://ask.sagemath.org/question/8983/why-is-3e1-not-equivalent-to-30/</link><description>I thought that 3e1 is completely equivalent to 30.
However, it is not:
sage: (1/30).n(digits=30)
0.0333333333333333333333333333333
sage: (1/3e1).n(digits=30)
0.0333333333333333328707404064062
Then I thought that 3e1 is always 53-bit real number or something like that.
But I was wrong again:
sage: 1/3e1.n(digits=30)
0.0333333333333333333333333333333
Now I am just confused. Is this a bug? If not, how should I
understand the second input above, and where can I find it documented? (Sage 5.0)</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">kkumer</dc:creator><pubDate>Fri, 01 Jun 2012 07:47:51 +0200</pubDate><guid>https://ask.sagemath.org/question/8983/</guid></item><item><title>Arbitrary Precision Physics Calculation</title><link>https://ask.sagemath.org/question/8719/arbitrary-precision-physics-calculation/</link><description>I would like to do some physics problems in high precision. I cannot find any examples or sample worksheets that are accessable on a basic level. I just want real numbers ( including large and small in scientific notation ) I am pretty sure this is not too hard, perhaps it is too simple to be explained? Any help would be appreciated.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">russ_hensel</dc:creator><pubDate>Wed, 15 Feb 2012 15:10:52 +0100</pubDate><guid>https://ask.sagemath.org/question/8719/</guid></item><item><title>Set global precision for reals?</title><link>https://ask.sagemath.org/question/7887/set-global-precision-for-reals/</link><description>Hello,
If this makes any difference, I am using the Sage Notebook.
I want to reuse a large piece of code. However, when I wrote it, the default precision seemed sufficient to me, and now I am encountering truncation errors. Can I specify a global precision at the beginning of the worksheet? My variable declarations are all like a,b=var('a,b').
Thanks!</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">chaesloc</dc:creator><pubDate>Thu, 20 Jan 2011 11:56:50 +0100</pubDate><guid>https://ask.sagemath.org/question/7887/</guid></item><item><title>HowTo Compute Past Largest Cython Supported Wordsize (efficiently)?</title><link>https://ask.sagemath.org/question/7600/howto-compute-past-largest-cython-supported-wordsize-efficiently/</link><description>Say I compute over a domain where my largest Cython cdef is ___ unsigned bits. Having enjoyed the wonderful Cython speedup this long, does Cython let me continue at arbitrary precisions past the largest supported word size? Any contrived example will do (for an answer, assuming it works!) Please and thank you very much.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ccanonc</dc:creator><pubDate>Fri, 20 Aug 2010 01:29:16 +0200</pubDate><guid>https://ask.sagemath.org/question/7600/</guid></item></channel></rss>