<?xml version="1.0" encoding="utf-8"?>
<rss xmlns:atom="http://www.w3.org/2005/Atom" version="2.0"><channel><title>ASKSAGE: Sage Q&A Forum - RSS feed</title><link>https://ask.sagemath.org/questions/</link><description>Q&A Forum for Sage</description><atom:link href="https://ask.sagemath.org/feeds/rss/" rel="self"></atom:link><language>en</language><copyright>Copyright Sage, 2010. Some rights reserved under creative commons license.</copyright><lastBuildDate>Thu, 14 Mar 2024 10:42:46 +0100</lastBuildDate><item><title>values of variables from points in the polyhedron defined by a linear program</title><link>https://ask.sagemath.org/question/55520/values-of-variables-from-points-in-the-polyhedron-defined-by-a-linear-program/</link><description>SageMath provides a [function](https://doc.sagemath.org/html/en/reference/numerical/sage/numerical/mip.html#sage.numerical.mip.MixedIntegerLinearProgram.polyhedron) for constructing the polyhedron defined by a linear program. Given a point in such a polyhedron, how can I tell which coordinate of the point corresponds to which variable of the linear program?
**ADDED:** The documentation suggests that "the polyhedron is built from the variables stored by the LP solver" and that "they usually match the ones created explicitly when defining the LP", except possibly for Gurobi solver. So, the question seems to reduce to finding the order number of each variable in LP (or an accurate bookkeeping of their creations). Things are even more fuzzy for Gurobi, which one of the best solvers out there.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Max Alekseyev</dc:creator><pubDate>Sun, 31 Jan 2021 19:51:48 +0100</pubDate><guid>https://ask.sagemath.org/question/55520/</guid></item><item><title>ring pb with Polyhedron</title><link>https://ask.sagemath.org/question/76482/ring-pb-with-polyhedron/</link><description> Hi
why is an error generated if I comment the line:
#lNew=[[0, 0, 0], [0, -1, 0], [1, -1, 0], [0, -1, 1]]
in the code below:
var('t_x',latex_name=r"\\teta_{x}")
Adic={0: [0, 0, 0], 1: [1, 0, 0], 2: [1, 1, 0], 3: [0, 1, 0] ,
4: [0, 0, 1], 5: [1, 0, 1], 6: [1, 1, 1], 7: [0, 1, 1]}
tetraHedron=[0, 4, 5, 7]
tetraHedronDic={}
for vertice in tetraHedron :
tetraHedronDic[vertice]=Adic.get(vertice)
angleRot=pi/2
rotX=matrix(SR,[[1,0,0],[0,cos(t_x),-sin(t_x)],[0,sin(t_x),cos(t_x)]])
newDic={}
for k in tetraHedronDic.keys() :
newDic[k]=list((rotX.subs(t_x=angleRot)*vector(tetraHedronDic.get(k))))
pOld=Polyhedron([tetraHedronDic.get(k) for k in tetraHedronDic.keys() ])
print('pOld vertices: ',pOld.integral_points())
lNew=[newDic.get(k) for k in newDic.keys() ]
print('lNew : ',lNew)
#lNew=[[0, 0, 0], [0, -1, 0], [1, -1, 0], [0, -1, 1]]
print('lNew : ',lNew)
pNew=Polyhedron(lNew)
print('pNew vertices : ',pNew.integral_points())
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ortollj</dc:creator><pubDate>Thu, 14 Mar 2024 10:42:46 +0100</pubDate><guid>https://ask.sagemath.org/question/76482/</guid></item><item><title>What is the algorithm used for polyhedra intersection?</title><link>https://ask.sagemath.org/question/74396/what-is-the-algorithm-used-for-polyhedra-intersection/</link><description> What is the algorithm used for polyhedra intersection and what is its time complexity?
Is the algorithm based on a research paper? If so, which one?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">muha123</dc:creator><pubDate>Mon, 20 Nov 2023 16:31:33 +0100</pubDate><guid>https://ask.sagemath.org/question/74396/</guid></item><item><title>Union of touching polyhedra</title><link>https://ask.sagemath.org/question/55769/union-of-touching-polyhedra/</link><description>Hi, I'm trying to do a union operation over multiple touching polyhedra into one but couldn't find how to achieve this with Sage. For example, how can I merge these two cubes and dissolve the interior face (the touching face):
# two cubes touching
cube_a = Polyhedron(vertices=[(0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1)])
cube_b = Polyhedron(vertices=[(1,1/2,0), (1,1/2,1), (1,3/2,0), (1,3/2,1), (2,1/2,0), (2,1/2,1), (2,3/2,0), (2,3/2,1)])
# visualize
cube_a.plot() + cube_b.plot()
The polyhedra can be assumed all convex, and each touching pair share a polygon interface. I found polyhedron.intersection(other), but no polyhedron.union(other) or so. Any workaround I can do? Thanks in advance.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">zhaiyu</dc:creator><pubDate>Fri, 19 Feb 2021 13:55:30 +0100</pubDate><guid>https://ask.sagemath.org/question/55769/</guid></item><item><title>Checking whether a fan is projective: any way to get it faster?</title><link>https://ask.sagemath.org/question/61045/checking-whether-a-fan-is-projective-any-way-to-get-it-faster/</link><description>I need to check whether a certain complete fan in R^3 is projective or not. What I tried was export the fan to macaulay2, and apply isPolytopal. However, while completeness is checked in like 30 sec, the polytopality gets stuck, the program doesn't finish in any reasonable time (we left it running for the night, with no result). My question is: are there any more effective ways of checking whether fans are polytopal or not?
Just in case, attached is my code:
macaulay2('loadPackage "Polyhedra"')
L = ToricLattice(4)
Q = ToricLattice(3)
h = L.hom([[1,0,0],[0,1,0],[0,0,1],[-1,-1,-1]],Q)
#rays in sage:
rays = [h((0,2,0,1)),h((0,3,0,2)),h((0,3,1,2)),h((0,5,2,3)),h((0,4,1,2)),h((0,1,0,1)),h((0,1,1,1)),h((0,3,2,2)),h((0,2,1,1)),h((0,0,0,1)),h((0,0,1,1)),h((0,0,1,0)),h((0,3,1,1)),h((1,0,1,1)),h((0,1,0,0)),h((1,0,0,1)),h((1,0,0,0)),h((1,3,0,1)),h((0,4,0,1)),h((1,1,0,1)),h((2,3,0,2)),h((1,2,0,1)),h((0,3,0,1)),h((1,3,0,2)),h((2,5,0,3)),h((1,4,0,2)),h((0,5,0,2))]
#exporting rays to Macaulay
raylist = []
for i in rays:
a = i[0]
b = i[1]
c = i[2]
raylist.append(macaulay2(f'{a},{b},{c}'))
newraylist = []
for i in raylist:
newraylist.append(macaulay2(f'toList{i}'))
#cones in sage:
cones=[(1,2,6),(2,3,6),(3,4,8),(1,5,6),(3,6,7),(3,7,8),(5,6,9),(6,7,11),(7,8,11),(6,9,10),(6,10,11),(8,11,12),(8,12,18),(10,11,13),(11,12,14),(11,13,16),(11,14,16),(13,15,16),(14,16,17),(15,16,19),(16,17,21),(17,18,21),(16,19,20),(16,20,21),(18,21,22),(19,20,24),(20,21,24),(21,22,26),(19,23,24),(21,24,25),(21,25,26),(0,2,3,4),(12,14,17,18),(9,10,13,15),(9,15,19),(8,18,22),(5,9,19),(1,5,19),(1,19,23),(0,1,2,23),(0,23,24,25),(22,26,8),(0,4,25,26),(4,8,26)]
#creating the fan in macaulay with cones as above
macaulay2('Z = coneFromVData matrix {{0,0,0},{0,0,0},{0,0,0}}')
macaulay2('F = fan Z')
conelist = []
for cone in cones:
if len(cone) == 3:
macaulay2(f'v1 = vector {newraylist[cone[0]]}');
macaulay2(f'v2 = vector {newraylist[cone[1]]}');
macaulay2(f'v3 = vector {newraylist[cone[2]]}');
macaulay2('C = coneFromVData matrix {v1,v2,v3}');
macaulay2('F = addCone(C,F)')
if len(cone) == 4:
macaulay2(f'v1 = vector {newraylist[cone[0]]}');
macaulay2(f'v2 = vector {newraylist[cone[1]]}');
macaulay2(f'v3 = vector {newraylist[cone[2]]}');
macaulay2(f'v4 = vector {newraylist[cone[3]]}');
macaulay2('C = coneFromVData matrix {v1,v2,v3,v4}');
macaulay2('F = addCone(C,F)')
#checking completeness and polytopality
macaulay2('isComplete F')
macaulay2('isPolytopal F')</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Polydarya</dc:creator><pubDate>Thu, 10 Feb 2022 14:55:45 +0100</pubDate><guid>https://ask.sagemath.org/question/61045/</guid></item><item><title>To find the ordered vertices of the faces of a 3D polyhedron with Vrepresentation</title><link>https://ask.sagemath.org/question/60760/to-find-the-ordered-vertices-of-the-faces-of-a-3d-polyhedron-with-vrepresentation/</link><description> I have this list of vertices of a polyhedron in 3D.
V=[[0.00, 0.00, 2.0],
[1.0, 0.31, 1.0],
[1.2, 0.00, 0.62],
[1.0, 0.00, 0.00],
[0.078, 0.31, 2.0],
[0.00, 0.31, 2.0],
[0.00, 0.62, 0.00],
[0.00, 0.00, 0.00],
[0.00, 0.88, 0.50]]
Thoses vertices define some faces listed in the following list
F= [[0.00, 0.00, 2.0],
[1.0, 0.31, 1.0],
[1.2, 0.00, 0.62],
[1.0, 0.00, 0.00],
[0.078, 0.31, 2.0],
[0.00, 0.31, 2.0],
[0.00, 0.62, 0.00],
[0.00, 0.00, 0.00],
[0.00, 0.88, 0.50]]
Sage is able to gives a list for indexes of vertices wghich belongs to a face :
fC=[[0, 2, 4, 6],
[0, 1, 4, 5],
[0, 1, 2, 3],
[1, 3, 5, 7],
[2, 3, 6, 7],
[4, 5, 6, 7]]
but unfortunately the indices are not necessarily given in the good order that gives the convex hull of each sublist of vertices in `fc`. I know the adjacency matrix of polyhedron which is
A=[[0 1 1 0 1 0 0 0],
[1 0 0 1 0 1 0 0],
[1 0 0 1 0 0 1 0],
[0 1 1 0 0 0 0 1],
[1 0 0 0 0 1 1 0],
[0 1 0 0 1 0 0 1],
[0 0 1 0 1 0 0 1],
[0 0 0 1 0 1 1 0]]
I am a bad programmer and I do not know how to find the good permutation of the sublist in `fc` (Perhaps ther is a simple way that the one I suggest). I need help. Thanks in advance.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Cyrille</dc:creator><pubDate>Sat, 22 Jan 2022 10:47:09 +0100</pubDate><guid>https://ask.sagemath.org/question/60760/</guid></item><item><title>Create polyhedron for given matrix A and vector b</title><link>https://ask.sagemath.org/question/60478/create-polyhedron-for-given-matrix-a-and-vector-b/</link><description>> P(A,b)={x∣ A.x ≤ b}
I have to create a polyhedron with this inputs
but in sage inequalities like this
> A.x + b >= 0
, how to convert</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">XLVII</dc:creator><pubDate>Thu, 30 Dec 2021 19:58:55 +0100</pubDate><guid>https://ask.sagemath.org/question/60478/</guid></item><item><title>How to use LRS engine in Sage?</title><link>https://ask.sagemath.org/question/60174/how-to-use-lrs-engine-in-sage/</link><description>I run Sage on my MacOS using terminal. As part of a project I am doing, I need to use the lrs engine:
def getVolume(self,eng='lrs'):
"""
needs Sage 5.9 for 'lrs' engine
"""
return self.poly.volume(engine=eng)*factorial(self.poly.dim())
However, this getVolume() function does not seem to work and always returns 0. So, I did some research and I am pretty sure my system does not have the Lrs engine at all. I checked for Lrs using this code: https://doc.sagemath.org/html/en/reference/misc/sage/features/lrs.html and it told me that Lrs is not there.
I am quite confused about this since I downloaded Sage very recently (just 1-2 months ago) and it should be there? Am I doing something wrong? If it needs to be installed, how would I go about downloading this library so I can use it?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">asdfsa</dc:creator><pubDate>Thu, 09 Dec 2021 14:34:17 +0100</pubDate><guid>https://ask.sagemath.org/question/60174/</guid></item><item><title>Ranging the Z axis</title><link>https://ask.sagemath.org/question/55355/ranging-the-z-axis/</link><description>I am plotting arrangements of hyperplanes. Like this one:
H3.<x, y, z> = HyperplaneArrangements(QQ)
A = H3([(1, 2, 1), 0],
[(-4, -3, -2), 0],
[(3, 3, -2), 0],
[(1, -4, 3), 0],
[(-2, 2, 1), 0])
A.plot(ranges=[(-1, 1), (-1, 1)], aspect_ratio=(1, 1, 0.25))
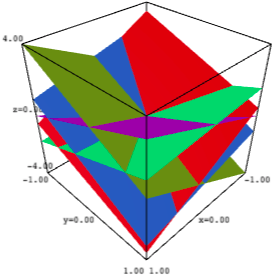
The problem is I need the z axis to range from -1 to 1 rather than from -4 to 4.
Is there a way to change that?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Lars</dc:creator><pubDate>Tue, 19 Jan 2021 15:36:01 +0100</pubDate><guid>https://ask.sagemath.org/question/55355/</guid></item><item><title>A certain polyhedron-related computation: any way to get it quicker?</title><link>https://ask.sagemath.org/question/57082/a-certain-polyhedron-related-computation-any-way-to-get-it-quicker/</link><description>(This is a white flag sort of question.) I have a numeric conjecture that I was trying to verify. The conjecture is this:
- take a polyhedron P whose vertices are a poset
- extend this to a (non-reflexive) operation on all faces by saying that F is smaller than G if max vertex of F is
smaller than min vertex of G
- take an algebra R of rational functions on generators x_F for all faces of P, plus extra generator t
- define the following endomorphism f of R:
- for a face F, let Ch(F) be the set of all chains in F, where for a chain C = F1 <... < Fn its total codimension is codim(F,C) = dimF - sum dim Fi
- for a chain C = F1 < ... < Fn, define its monomial m(C) by taking the product of either x_Fi, if dim F_i>0, or of x_Fi/(1-x_Fi), if Fi is a vertex, and then times t^{codim(F,C)}
- define f by sending x_F to the sum of m(C) for all chains C in Ch(C)
- additionally define an endomorhism I by sending x_F to -x_F and t to -t
CONJECTURE: *very often* f*I will be an involution.
The conjecture is proved for simplices, cubes, and all polygons. It's also disproved in some cases. A key example where I need to know the answer is the associahedron, with Tamari order on vertices.
I've asked several questions here and, thanks to tmonteil, wrote a code that checks the conjecture for the 3D associahedron -- and... my code can't run in any reasonable amount of time! Does the problem above sound like something computationally approachable, given that the number of chains in the 3-dimensional face of associahedron is equal to 22663?
How would you write this code?
Attached, my (very bad) code:
---
import itertools
A = Polyhedron(vertices = [[1,2,6,1],[1,6,2,1],[2,1,6,1],[1,2,3,4],[1,4,1,4],[1,6,1,2],[2,1,3,4],[4,1,4,1],[4,3,2,1],[4,3,1,2],[3,1,2,4],[3,2,1,4],[4,1,2,3],[4,2,1,3]])
Fempty = list(A.face_generator())
F = []
for i in Fempty:
if i.dim() != -1:
F.append(i)
R = Frac(PolynomialRing(QQ,x,len(F)+1))
R.inject_variables()
face = {x:f for x,f in list(zip(R.gens(),F))}
x = {f:x for x,f in list(zip(R.gens(),F))}
V = VectorSpace(QQ,4)
W = Cone([[1,-1,0,0],[1,0,-1,0],[1,0,0,-1],[0,1,-1,0],[0,1,0,-1],[0,0,1,-1]])
elms = A.vertices()
rels = []
for i in A.faces(1):
Li = i.vertices()
if vector(list(Li[0]))-vector(list(Li[1])) in W:
rels.append([Li[0],Li[1]])
else:
rels.append([Li[1],Li[0]])
P = Poset((elms, rels), cover_relations = True, facade = True)
def flarger(f1,f2):
L1 = f1.vertices()
L2 = f2.vertices()
for v in L1:
for w in L2:
if (P.lt(w,v) or v == w) == False:
return False
return True
bigelms = A.faces(0)+A.faces(1)+A.faces(2)+A.faces(3)
bigrels = []
for i in bigelms:
for j in bigelms:
if (flarger(i,j) and i != j):
bigrels.append([i,j])
Q = Poset((bigelms, bigrels), cover_relations = False, facade = True)
elll = list(x[i] for i in bigelms)
relll = []
for i in bigrels:
relll.append([x[i[0]],x[i[1]]])
QQ = Poset((elll, relll), cover_relations = False, facade = True)
def inside(f1,f2):
L1 = face[f1].vertices()
L2 = face[f2].vertices()
for v in L1:
if v not in L2:
return False
return True
def subfaces(feis):
result = []
for item in elll:
if inside(item,feis):
result.append(item)
return result
def sfposet(feis):
Res = Poset(QQ.subposet(subfaces(feis)),facade = True)
return Res
def chains(myx):
Huj = sfposet(myx).chains()
result = []
for i in Huj:
if i != []:
result.append(i)
return result
def p(feis):
answer = feis
if face[feis].dim() == 0:
answer = feis/(1-feis)
return answer
def monprod(monlist):
answer = 1
for item in monlist:
answer = answer*p(item)
return answer
def chdim(ch):
dim = 0
for item in ch:
dim = dim+face[item].dim()
return dim
def fmap(feis):
answer = 0
dimf = face[feis].dim()
Flist = chains(feis)
for item in Flist:
power = dimf - chdim(item)
answer = answer + monprod(item)*(x45^power)
return answer
minuslist = []
for feis in F:
minuslist.append(-x[feis])
minuslist.append(-x45)
fmaplist = []
for feis in F:
fmaplist.append(fmap(x[feis]))
fmaplist.append(x45)
f = R.hom(fmaplist)
I = R.hom(minuslist)
f*I*f*I</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Polydarya</dc:creator><pubDate>Wed, 12 May 2021 01:17:44 +0200</pubDate><guid>https://ask.sagemath.org/question/57082/</guid></item><item><title>Subfaces of a face in Polyhedra package?</title><link>https://ask.sagemath.org/question/57069/subfaces-of-a-face-in-polyhedra-package/</link><description>I'm using polyhedra package and I need the operation that, for a given face, provides the list of all its subfaces (as faces in the bigger polyhedron). If I'm doing something like face.as_polyhedron().faces(n), the faces stop being recognised as belonging to the bigger polyhedron. What is the correct way to do that?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Polydarya</dc:creator><pubDate>Tue, 11 May 2021 15:58:50 +0200</pubDate><guid>https://ask.sagemath.org/question/57069/</guid></item><item><title>In Sage is there support for non-convex polyhedra?</title><link>https://ask.sagemath.org/question/50929/in-sage-is-there-support-for-non-convex-polyhedra/</link><description> Which reference page gives help or examples? Can they be triangulated? I want to triangulate them in order to help turn them into stl files.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">dart2163</dc:creator><pubDate>Wed, 22 Apr 2020 22:46:11 +0200</pubDate><guid>https://ask.sagemath.org/question/50929/</guid></item><item><title>Oriented vertices of Polyhedron</title><link>https://ask.sagemath.org/question/56186/oriented-vertices-of-polyhedron/</link><description> Hi, I wonder what is the most convenient way to extract the ordered/oriented vertices of a Polyhedron/PolyhedronFace.
Specifically, say that we have a cube:
sage: cb = Polyhedron(vertices=[(0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1)])
which consists of 6 facets:
sage: cb.facets()
(A 2-dimensional face of a Polyhedron in ZZ^3 defined as the convex hull of 4 vertices,
A 2-dimensional face of a Polyhedron in ZZ^3 defined as the convex hull of 4 vertices,
A 2-dimensional face of a Polyhedron in ZZ^3 defined as the convex hull of 4 vertices,
A 2-dimensional face of a Polyhedron in ZZ^3 defined as the convex hull of 4 vertices,
A 2-dimensional face of a Polyhedron in ZZ^3 defined as the convex hull of 4 vertices,
A 2-dimensional face of a Polyhedron in ZZ^3 defined as the convex hull of 4 vertices)
I can easily know the indices of vertices (in `cb.Vrepresentation`) that form each facets, e.g., for the first facet:
sage: cb.facets()[0].ambient_V_indices()
(0, 1, 4, 5)
However, the four vertices are not properly ordered (linked) as I inspect the adjacency matrix:
sage: cb.vertex_adjacency_matrix()
[0 1 1 0 1 0 0 0]
[1 0 0 1 0 1 0 0]
[1 0 0 1 0 0 1 0]
[0 1 1 0 0 0 0 1]
[1 0 0 0 0 1 1 0]
[0 1 0 0 1 0 0 1]
[0 0 1 0 1 0 0 1]
[0 0 0 1 0 1 1 0]
(from the adjacent matrix the ordered indices of the four vertices should be 0->1->5->4, or reversed as 4->5->1->0).
The proper orientation of the vertices is needed for B-rep. Though I can extract the proper ordering with `vertex_adjacency_matrix()`, how to make sure they're consistently CCW orientated (seen from outside) still confuses me.
I'm kinda sure these are well managed in Sage, because the `obj_repr()` method in [plot3d](https://doc.sagemath.org/html/en/reference/plot3d/sage/plot/plot3d/base.html?highlight=obj_repr#sage.plot.plot3d.base.Graphics3d.obj_repr) seems working well providing a consistent facet-vertex representation:
sage: cb_render = cb.render_solid()
sage: cb_render.obj_repr(cb_render.default_render_params())
['g obj_1',
'usemtl texture7',
['v 0 0 0',
'v 0 0 1',
'v 0 1 0',
'v 0 1 1',
'v 1 0 0',
'v 1 0 1',
'v 1 1 0',
'v 1 1 1'],
['f 8 4 2 6',
'f 7 3 4 8',
'f 8 6 5 7',
'f 3 1 2 4',
'f 5 1 3 7',
'f 6 2 1 5'],
['f 6 2 4 8',
'f 8 4 3 7',
'f 7 5 6 8',
'f 4 2 1 3',
'f 7 3 1 5',
'f 5 1 2 6']]
(notice that the vertex index in OBJ representation starts from 1 instead of 0; the line `f 6 2 1 5` corresponds to the ordering `4->5->1->0` that I want)
Is there a native method for Polyhedron or PolyhdronFace that I can directly use for this?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">zhaiyu</dc:creator><pubDate>Tue, 16 Mar 2021 18:20:01 +0100</pubDate><guid>https://ask.sagemath.org/question/56186/</guid></item><item><title>Polyhedra, facets and vertices</title><link>https://ask.sagemath.org/question/55597/polyhedra-facets-and-vertices/</link><description>I have a 6-dimensional, convex, compact polyhedron in $\mathbb{R}^{12}$, that I am calling `P1`.
The polyhedron `P1` was specified by giving a large number of inequalities.
When I enter `P1.faces(5)` into Sage, I get the following
(A 5-dimensional face of a Polyhedron in RDF^12 defined as the convex hull of 6 vertices,
A 5-dimensional face of a Polyhedron in RDF^12 defined as the convex hull of 7 vertices,
A 5-dimensional face of a Polyhedron in RDF^12 defined as the convex hull of 7 vertices,
A 6-dimensional face of a Polyhedron in RDF^12 defined as the convex hull of 7 vertices,
A 5-dimensional face of a Polyhedron in RDF^12 defined as the convex hull of 6 vertices,
A 6-dimensional face of a Polyhedron in RDF^12 defined as the convex hull of 8 vertices,
...)
How can there be two 6-dimensional faces, each with a different number of vertices,
on the boundary of `P1`? I have checked that `P1` really does have dimension 6.
Also, when I try to find a list of vertices on the boundary of any 5-dimensional face of `P1`,
for example
P1.faces(5)[0].vertices_list()
I get an error message
AttributeError: 'tuple' object has no attribute 'vertices_list'
However, `P1.faces(5)[0].vertices()` works.
My second question is, how do I get a list of vertices on the boundary of an $n$-dimensional face?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Ingrid</dc:creator><pubDate>Sat, 06 Feb 2021 10:10:56 +0100</pubDate><guid>https://ask.sagemath.org/question/55597/</guid></item><item><title>Find complementary cones from a cone</title><link>https://ask.sagemath.org/question/54256/find-complementary-cones-from-a-cone/</link><description>Suppose I have a cone constructed from a set of points. In 2d for instance:
cone1 = Cone([[-1, 4], [4, -1]])
The rays of this `cone1` are exactly those two vectors I used to define the cone.
Now, I take the cone
cone2 = Cone([[1, 0], [0, 1]])
Again its rays are given by the two vectors used to define it.
Now, `cone1` contains `cone2`, and its intersection with `cone2` is exactly `cone2`.
I would like to know if there is a way to extract the complementary cones from `cone1` "subtracting" `cone2`. Basically I would need:
cone3 = Cone([[-1, 4], [0, 1]])
and
cone4 = Cone([[1, 0], [4, -1]])
Is there a way to extract these cones?
I know that in the 2d example I can plot the cones with .plot() and subtract them visualizing them, of course this is an example. What I would like to know if there is an algorithmic way to extract all the "complementary cones" from a bigger cone that contains (completely) another cone. So I would like to find a way to define `cone3` and `cone4` in higher dimensions, and "algorithmically".</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">amininno</dc:creator><pubDate>Tue, 17 Nov 2020 09:29:43 +0100</pubDate><guid>https://ask.sagemath.org/question/54256/</guid></item><item><title>Parallelizing Polyhedral volume computation</title><link>https://ask.sagemath.org/question/36859/parallelizing-polyhedral-volume-computation/</link><description> For an application, I need to compute volumes of convex polytopes of dimension of about 300. The polytopes of interest have a restricted form:
$$
P:=\{ (x_1,x_2,\ldots,x_n) \} ~\text{with} \\
0\leq x_i\leq x_{i+1} \leq L,\\
l\leq x_i - x_{i+1} \leq u
$$
where $L,u,l$ are known positive constants.
On my laptop, the polytope volume computation routine takes about 3 hours to compute for $n=9$, and freezes for larger $n$, making it useless for most interesting cases of my application.
> Is there an easy way to parallelize the volume routine?
Perhaps by a straightforward use of the [multiprocessing] module, when running on a cluster ?
A more advanced use case, which also arises in my application, lies in computing integrals over the polytope: $\int_{P} f(\mathbf{x}) d\mathbf{x}$, where $f$ is a symmetric function of its arguments. I would greatly be interested in techniques that extend to this case as well.
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">dracoTheDragon</dc:creator><pubDate>Wed, 08 Mar 2017 07:00:25 +0100</pubDate><guid>https://ask.sagemath.org/question/36859/</guid></item><item><title>What is the most efficient way to "look up" a face in the face lattice of a polyhedron?</title><link>https://ask.sagemath.org/question/34485/what-is-the-most-efficient-way-to-look-up-a-face-in-the-face-lattice-of-a-polyhedron/</link><description>Say I have a polyhedron `p` with face lattice `L = p.face_lattice()`. I want to define `x` as the element of `L` defined as the convex hull of vertices `<0 1 3>` of `p`. What is the most efficient way to define `x`?
For example, consider
sage: p = polytopes.simplex(3)
sage: for v in p.vertices():
print '\tIndex {}:'.format(v.index()), v
....:
Index 0: A vertex at (0, 0, 0, 1)
Index 1: A vertex at (0, 0, 1, 0)
Index 2: A vertex at (0, 1, 0, 0)
Index 3: A vertex at (1, 0, 0, 0)
We see that `p` has four vertices.
The vertices indexed by `0`, `1`, and `3` are the vertices of a face of `p`. This is confirmed:
sage: L = p.face_lattice()
sage: list(L)
[<>,
<0>,
<1>,
<2>,
<3>,
<0,1>,
<0,2>,
<1,2>,
<0,3>,
<1,3>,
<2,3>,
<0,1,2>,
<0,1,3>,
<0,2,3>,
<1,2,3>,
<0,1,2,3>]
I want to define `x` as the face in `p.face_lattice()` given by these vertices. Of course, I could do this by hand with `x = list(L)[12]`, but I want a way to automate this.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">done_with_fish</dc:creator><pubDate>Tue, 16 Aug 2016 11:06:34 +0200</pubDate><guid>https://ask.sagemath.org/question/34485/</guid></item><item><title>Projection along affine hull</title><link>https://ask.sagemath.org/question/35487/projection-along-affine-hull/</link><description>Let `n_1,...,n_r` be integral points in a polyhedron `P`. The paper I am reading refers to "the projection of `P` along `aff(n_1,...,n_r)`". Here `aff(n_1,...,n_r)` is the affine hull of `n_1,...,n_r`. Can I accomplish this projection in sage?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">done_with_fish</dc:creator><pubDate>Tue, 08 Nov 2016 20:09:57 +0100</pubDate><guid>https://ask.sagemath.org/question/35487/</guid></item><item><title>VoronoiDiagram returns empty regions</title><link>https://ask.sagemath.org/question/49749/voronoidiagram-returns-empty-regions/</link><description>Dear all,
Given the set of 2 points
P = [[-2687.19000000000, -2088.53000000000], [-2686.81000000000, -2084.19000000000]]
I would like to compute the voronoi diagram of $P$. When doing so i saw that the regions of the voronoi are:
{P(-2687.19000000000, -2088.53000000000): The empty polyhedron in RDF^0,
P(-2686.81000000000, -2084.19000000000): A 1-dimensional polyhedron in RDF^2 defined as the convex hull of 1 vertex and 1 ray}
In my code, I do need that those regions are not empty! Why is this happening and how can i fix it?
Please advise and thanks in advance.
P.s. Note that when I make the points a little I get that the voronoi is not empty.
Full Code:
P = [[-2687.19, -2088.53], [-2686.81, -2084.19]]
V = VoronoiDiagram(P)
R = V.regions()</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">muradtuk</dc:creator><pubDate>Sun, 02 Feb 2020 17:43:31 +0100</pubDate><guid>https://ask.sagemath.org/question/49749/</guid></item><item><title>Computing projection of a polyhedron</title><link>https://ask.sagemath.org/question/48155/computing-projection-of-a-polyhedron/</link><description>How to compute the projection of a given polyhedron onto a given smaller-dimensional plane?
E.g., the projection of Polyhedron(vertices=[(-1,-1), (1,3), (5,-2)]) onto the line $y=x$.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Max Alekseyev</dc:creator><pubDate>Thu, 03 Oct 2019 02:08:37 +0200</pubDate><guid>https://ask.sagemath.org/question/48155/</guid></item><item><title>About algorithm for testing whether a point is in a V-polyhedron</title><link>https://ask.sagemath.org/question/48462/about-algorithm-for-testing-whether-a-point-is-in-a-v-polyhedron/</link><description> Hi there,
I have two questions and I wonder if any of you may know the answer.
1 What algorithm does sage use to test whether a given point is in a polyhedron, namely in the function polyhedron.contains()?
2. Is there a difference in the algorithm according to whether the V-polyhedron is a V-polytope or is unbounded?
Thank you, and best regards,
Guillermo</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">guillermo</dc:creator><pubDate>Tue, 22 Oct 2019 11:42:20 +0200</pubDate><guid>https://ask.sagemath.org/question/48462/</guid></item><item><title>How to find the vertices a a polyhedron define by inequalities ,</title><link>https://ask.sagemath.org/question/48144/how-to-find-the-vertices-a-a-polyhedron-define-by-inequalities/</link><description>I would like to know if there is a way to obtain the v-representation of a polyhedron from its definition by inequalities like
$\{x \geq 0, y \geq 0, y + x \leq 10\}$
I find the opposite in the documentation. (If possible in higher dimension, because i can always solve for the solution.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Cyrille</dc:creator><pubDate>Wed, 02 Oct 2019 19:02:40 +0200</pubDate><guid>https://ask.sagemath.org/question/48144/</guid></item><item><title>Memory leak in Polyhedron?</title><link>https://ask.sagemath.org/question/47243/memory-leak-in-polyhedron/</link><description>If I run the following code:
import gc
while True:
P = Polyhedron([[1,0,0,0], [0,1,0,0], [0,0,1,0], [0,0,0,1]])
faces = P.faces(3)
del P, faces
print "memory usage: " + str(get_memory_usage()) + ", gc: " + str(gc.collect())
the memory usage keeps increasing.
Do you know what is the cause and how to avoid this problem?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Giove</dc:creator><pubDate>Mon, 22 Jul 2019 16:15:08 +0200</pubDate><guid>https://ask.sagemath.org/question/47243/</guid></item><item><title>Looking for stellation of polyhedra</title><link>https://ask.sagemath.org/question/45291/looking-for-stellation-of-polyhedra/</link><description> Hi Sagists,
I'm wondering if anyone knows a way to do stellation with the Polyhedron class?
Mathematica has a Stellate function but they admit it is really an augment operation and not a true stellation
thanks
Pat Browne
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">PatB</dc:creator><pubDate>Sun, 03 Feb 2019 18:45:06 +0100</pubDate><guid>https://ask.sagemath.org/question/45291/</guid></item><item><title>Global Dependency in Polyhedron Volume</title><link>https://ask.sagemath.org/question/44695/global-dependency-in-polyhedron-volume/</link><description> Hi all,
I am new to sage and want to use it in one of my python scripts to calculate the volume of higher dimensional polyhedrons. When executing my script I get a "ZeroDivisionError" for some of the polyhedrons. However when run in an individual script they work perfectly fine as long as there is no other calculation beforehand.
Here is an example, the file is called DebugSageVolume.py and I execute it with "sage -python DebugSageVolume.py" under Ubuntu 18.04, SageMath version 8.1
#!/usr/lib/python2.7/dist-packages/sage -python
from sage.all import *
# this works fine
matrix1 = matrix(RR, [[0, 1, 0, 0, 0], [1, -1, 0, 0, 0],
[0, 0, 1, 0, 0], [1, 0, -1, 0, 0],
[0, 0, 0, 1, 0], [1, 0, 0, -1, 0],
[0, 0, 0, 0, 1], [1, 0, 0, 0, -1],
[0.5, -0.5, -0.5, -0.5, -0.5], [-0.5, 0.5, 0.5, 0.5, 0.5]])
poly1 = Polyhedron(ieqs=matrix1)
volume1 = poly1.volume(measure="induced")
print(volume1)
#this results in an error when executed after the above. But when commenting the above this works fine
matrix2 = matrix(RR, [[0, 1, 0, 0, 0], [1, -1, 0, 0, 0],
[0, 0, 1, 0, 0], [1, 0, -1, 0, 0],
[0, 0, 0, 1, 0], [1, 0, 0, -1, 0],
[0, 0, 0, 0, 1], [1, 0, 0, 0, -1],
[0.75, -0.5, -0.5, -0.5, -0.5], [-0.75, 0.5, 0.5, 0.5, 0.5]])
poly2 = Polyhedron(ieqs=matrix2)
volume2 = poly2.volume(measure="induced")
print(volume2)
Any help would be greatly appreciated, thank you.
Michael</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">MichaelR</dc:creator><pubDate>Mon, 17 Dec 2018 19:10:30 +0100</pubDate><guid>https://ask.sagemath.org/question/44695/</guid></item><item><title>Viewer 3D issues</title><link>https://ask.sagemath.org/question/44620/viewer-3d-issues/</link><description>I'm trying to draw some 3D polyhedra. A search has brought up
https://ask.sagemath.org/question/41910/viewer-3d-problem/
but I still can't get a live plot. I have constructed my polyhedron `V` from the `Polyhedron` class as an intersection of linear inequalities. The command `V.plot()` works by using the JMol engine, except that when I attempt to make it "live" all the edges and faces disappear and I have collection of vertices only.
I can also plot with tachyon; that works fine but doesn't allow rotating.
When I plot with threejs: `V.plot(viewer='threejs',online=True)` all it plots is the wireframe box surrounding the polyhedron; that is, the xyz "box" in which the polyhedron fits, but not the polyhedron itself.
So - how can I create a 3D polyhedron with a "live" plot that allows rotating? </description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Alasdair</dc:creator><pubDate>Mon, 10 Dec 2018 05:49:34 +0100</pubDate><guid>https://ask.sagemath.org/question/44620/</guid></item><item><title>Computing polyhedron from MIP</title><link>https://ask.sagemath.org/question/33782/computing-polyhedron-from-mip/</link><description> I want to run the following code (I'm using SAGE v6.10 release version 2015-12-18):
P = MixedIntegerLinearProgram()
x = P.new_variable()
A = random_matrix(RR, 3, 2);
P.add_constraint(A*x <= [2.1,1.5,0.4])
P.polyhedron()
However, it outputs the error message:
> AttributeError: type object 'float'
> has no attribute 'fraction_field'
I noticed that if instead of using real variables I use only integer variables, then it works fine. For instance:
P = MixedIntegerLinearProgram()
x = P.new_variable()
A = random_matrix(ZZ, 3, 2);
P.add_constraint(A*x <= [2,1,0])
P.polyhedron()
outputs:
> A 2-dimensional polyhedron in QQ^2
> defined as the convex hull of 1 vertex
> and 2 rays
What do you suggest to overcome this problem?
Thanks</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">mforets</dc:creator><pubDate>Tue, 14 Jun 2016 14:09:09 +0200</pubDate><guid>https://ask.sagemath.org/question/33782/</guid></item><item><title>why I get huge number in H-representation in sage?</title><link>https://ask.sagemath.org/question/43613/why-i-get-huge-number-in-h-representation-in-sage/</link><description> I have a set of vertices and I want to find a H-representation of them. I used sage to do that but I got weird number in the inequalities!
here is my code:
vert2 = [[1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1],[1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0],[0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3],[3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0],[0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1],[1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4],[4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3],[3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2],[2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3],[3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4],
[4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7],[7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6],[6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5],[5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4],[4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2,3],[3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1,2],
[2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0,1],[1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8,0],
[0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6,8],[8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7,6],
[6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0,7],[7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0,0],
[0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6,0],[0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3,6],
[6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2,3],[3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4,2],
[2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3,4],[4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2,3],
[3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1,2],[2,3,4,2,3,6,0,0,7,6,8,0,1,2,3,4,5,6,7,4,3,2,3,4,1,0,3,0,1,1]]
p2=Polyhedron(vertices = vert2)
p2
p2.Hrepresentation()
And here is the part of my answer:
A 29-dimensional polyhedron in ZZ^30 defined as the convex hull of 30 vertices
(An equation (1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1) x - 91 == 0, An inequality (0, -6643755617445331037202609358, -1115451987061522518725310169, -4620824246361587837443723580, -3077838211630051976366550554, -2958690652672660811230373721, -974408181934402275593859480, -3250586099217454711737435326, -1999390120369594790625124513, -1415422103472822894852139772, -2534807215524130595973233650, -2780858391260346768723034201, -4072521014492760746645432088, -1331138469264064061646992630, -4722885096499104848736533209, -3180475210961898948969228316, -3851685143879995858104878858, -3228011163515660410829231425, -3072642994521821646580427696, -1374868705058151838371429430, -4889037447034222629220355689, -2510460065219895800789661380, -2297947035840486945050864530, -3657717103544642567050992273, -3458628241192993528820697768, -295584745844116667823309878, -3868958368255490017832885737, -6000440427999093271578675404, 853080186343081392188416198, -2835167870342318913892483281) x + 260907258623794816872847788563 >= 0, An inequality (0, -3688248056685400306080899479, -853080186343081392188416198, -7496835803788412429391025556, -1968532173404603910913726367, -5473904432704669229632139778, -3930918397973133368554966752, -3811770839015742203418789919, -1827488368277483667782275678, -4103666285560536103925851524, -2852470306712676182813540711, -2268502289815904287040555970, -3387887401867211988161649848, -3633938577603428160911450399, -4925601200835842138833848286, -2184218655607145453835408828, -5575965282842186240924949407, -4033555397304980341157644514, -4704765330223077250293295056, -4081091349858741803017647623, -3925723180864903038768843894, -2227948891401233230559845628, -5742117633377304021408771887, -3363540251562977192978077578, -3151027222183568337239280728, -4510797289887723959239408471, -4311708427536074921009113966, -1148664932187198060011726076, -4722038554598571410021301935, -6853520614342174663767091602) x + 338537555581015223561993662581 >= 0, </description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">naghmeh_ms</dc:creator><pubDate>Fri, 07 Sep 2018 17:55:00 +0200</pubDate><guid>https://ask.sagemath.org/question/43613/</guid></item><item><title>Getting convex hull of a set of points and plotting the polygon</title><link>https://ask.sagemath.org/question/33548/getting-convex-hull-of-a-set-of-points-and-plotting-the-polygon/</link><description>I'm using sagemath cloud.
I'm trying to get the convex hull of a finite set of points, then plotting the polygon. If I just plot the polygon with the vertices directly, I don't get the vertices in the right order to make up a convex polygon (plots edges joining the wrong points). Then I found out about cyclic_sort_vertices_2d which I thought would sort the vertices into the right order, but that's giving me errors. I don't understand the meaning of the errors. Appreciate any help.
here's the relevant code:
hull = Polyhedron(vertices=thePoints);
hull.vertices();
cyclic_sort_vertices_2d(hull.vertices());
And I have this import line at the top of my code for cyclic sort:
from sage.geometry.polyhedron.plot import cyclic_sort_vertices_2d;
Here's my output:
(A vertex at (9464.0, 10816.0), A vertex at (8736.0, 7735.0), A vertex at (7904.0, 8736.0), A vertex at (11088.0, 5607.0), A vertex at (15552.0, 6480.0), A vertex at (8160.0, 9248.0), A vertex at (8568.0, 9792.0), A vertex at (11076.0, 10140.0), A vertex at (12852.0, 5355.0))
And errors:
Error in lines 28-30
Traceback (most recent call last):
File "/projects/sage/sage-6.10/local/lib/python2.7/site-packages/smc_sagews/sage_server.py", line 905, in execute
exec compile(block+'\n', '', 'single') in namespace, locals
File "", line 1, in <module>
File "/projects/sage/sage-6.10/local/lib/python2.7/site-packages/sage/geometry/polyhedron/plot.py", line 245, in cyclic_sort_vertices_2d
adjacency_matrix = Vlist[0].polyhedron().vertex_adjacency_matrix()
File "sage/misc/cachefunc.pyx", line 2215, in sage.misc.cachefunc.CachedMethodCallerNoArgs.__call__ (/projects/sage/sage-6.10/src/build/cythonized/sage/misc/cachefunc.c:14346)
self.cache = f(self._instance)
File "/projects/sage/sage-6.10/local/lib/python2.7/site-packages/sage/geometry/polyhedron/base.py", line 1847, in vertex_adjacency_matrix
return self._vertex_adjacency_matrix()
File "/projects/sage/sage-6.10/local/lib/python2.7/site-packages/sage/geometry/polyhedron/base.py", line 312, in _vertex_adjacency_matrix
face_lattice = self.face_lattice()
File "sage/misc/cachefunc.pyx", line 2215, in sage.misc.cachefunc.CachedMethodCallerNoArgs.__call__ (/projects/sage/sage-6.10/src/build/cythonized/sage/misc/cachefunc.c:14346)
self.cache = f(self._instance)
File "/projects/sage/sage-6.10/local/lib/python2.7/site-packages/sage/geometry/polyhedron/base.py", line 3172, in face_lattice
face_constructor=face_constructor, required_atoms=atoms_vertices)
File "/projects/sage/sage-6.10/local/lib/python2.7/site-packages/sage/geometry/hasse_diagram.py", line 182, in Hasse_diagram_from_incidences
for coatom, atoms in enumerate(coatom_to_atoms)]
KeyError: (frozenset([]), frozenset([0]))</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ameetnsharma</dc:creator><pubDate>Thu, 26 May 2016 05:45:37 +0200</pubDate><guid>https://ask.sagemath.org/question/33548/</guid></item><item><title>find one interior point of a polyhedron</title><link>https://ask.sagemath.org/question/10829/find-one-interior-point-of-a-polyhedron/</link><description>Hi,
I have a bunch of inequations and I would like to know if there is a solution. What is the simplest way to achieve this in Sage ? I tried using MILP with success... but the point returned is not very fancy (often on the boundary). In an ideal world, I would like to optimize some quadratic function in order for the solution to be the nicest possible.
Here is a sample and simple example with only one inequality (other constraints are equalities) where I reproduced the output of MILP:
Constraints:
2.0 <= x_0 + x_7 + x_8 <= 2.0
2.0 <= x_1 + x_2 <= 2.0
2.0 <= x_3 + x_5 + x_9 <= 2.0
2.0 <= x_4 + x_6 <= 2.0
1.0 <= x_0 + x_2 + x_9 <= 1.0
1.0 <= x_5 + x_6 + x_8 <= 1.0
0.0 <= x_2 + x_6 <= 1.0
Variables:
x_0 is a continuous variable (min=0.0, max=2.0)
x_1 is a continuous variable (min=0.0, max=2.0)
x_2 is a continuous variable (min=0.0, max=2.0)
x_3 is a continuous variable (min=0.0, max=2.0)
x_4 is a continuous variable (min=0.0, max=2.0)
x_5 is a continuous variable (min=0.0, max=2.0)
x_6 is a continuous variable (min=0.0, max=2.0)
x_7 is a continuous variable (min=0.0, max=2.0)
x_8 is a continuous variable (min=0.0, max=2.0)
x_9 is a continuous variable (min=0.0, max=2.0)
There are plenty of *nice* solutions, one is
x0 = x2 = x5 = x6 = x8 = 1/3
x1 = x4 = 5/3
x3 = x7 = 4/3
But with the solver I got:
sage: p.solve()
sage: p.get_values(p[1],p[2],p[3],p[4],p[5],p[6],p[7],p[8],p[9])
[1, 2, 0, 2, 2, 0, 0, 0, 1]
Thanks</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">vdelecroix</dc:creator><pubDate>Fri, 13 Dec 2013 08:39:30 +0100</pubDate><guid>https://ask.sagemath.org/question/10829/</guid></item></channel></rss>